Выдающийся французский физик Луи де Бройль написал, по меньшей мере, две великих формулы: выражение для волновой функции свободной квантовой частицы, носящей его имя, где обобщил выражения для импульса и энергии квантовой частицы на случай когда масса покоя не равна нулю и соотношение
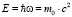. (1)
Смысл этой формулы заключается в том, что элементарная частица с массой покоя m0 имеет собственную квантовую энергию движения с частотой ω. Эта формула предложена де Бройлем в 1923 году в своей докторской диссертации в виде гипотезы. В последующем он показал, что эта формула является инвариантной и удовлетворяет известным релятивистским преобразованиям, поскольку частота и масса частицы преобразуются по одинаковым законам и справедлива, в том числе, и при отсутствии поступательного движения квантовых частиц [1].
Используя уравнение Шрёдингера и формулу (1) можно получить описание двух квантовых состояний для атома водорода. Одно традиционное описание атома водорода, излагаемое в учебниках по квантовой механике, другое – новое, субатомное состояние.
Основные уравнения и их решения
Запишем уравнение Шрёдингера для атома водорода с учетом формулы (1) в соответствии с рис. 1.
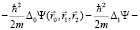
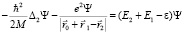. (2)
Здесь первое слагаемое описывает движение вероятностного центра электрона относительно вероятностного центра протона, который принят за начало координат. Второе слагаемое описывает собственное движение электрона относительно своего вероятностного центра за счет энергии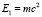 
. Третье слагаемое описывает собственное движение протона относительно собственного вероятностного центра с энергией 
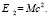Последнее слагаемое в левой части уравнения описывает кулоновское взаимодействие электрона с протоном. В уравнении (2) приняты обозначения: ε – энергия связи атома водорода, m, M – соответственно массы покоя электрона и протона.
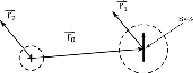
Рис. 1. Координаты атома водорода
Из уравнения (2) и рис. 1 можно видеть, что бы потенциальная энергия взаимодействия заряженных частиц в каждой точке была однозначна, нужно положить во всем пространстве:
. (3)
Тогда в уравнении (2) можно провести разделение переменных и записать его виде:
.
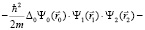
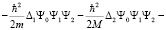
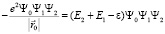Из этого уравнения получаем три уравнения. Первое уравнения является стандартным для описания атома водорода в нерелятивистском приближении и его решение приводится во всех учебниках по квантовой механике:
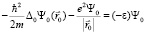. (4)
Второе и третье уравнения описывают собственное движение электрона и протона за счет энергий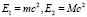 
,
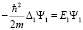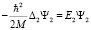. (5)
Решением этих уравнения являются стоячие неоднородные волны, затухающие на бесконечности и описывающие пространственную локализацию с учетом спина частиц [2]. Для электрона в нашем случае принято s = 1/2:
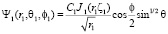. (6)
Здесь J1 – функция Бесселя первого порядка. Заметим, что согласно (3) и (5) спины заряженных частиц в атоме водорода должны быть коллинеарные и иметь одинаковое направление. Таким образом, суммарный спин атома водорода равен единице.
Рассмотрим другой частный случай, когда вероятностные центры локализации совпадают,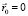 
. Это возможно, поскольку волновые функции собственного движения квантовых частиц в вероятностных центрах локализации равны нулю. Тогда из (2) получаем уравнение:
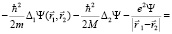
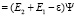. (7)
Уравнение (7) можно представить в виде двух уравнений, если сделать замену переменных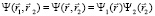 
, где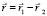 
и провести разделение переменных, получим:
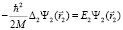(8)
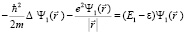. (9)
Уравнение (8) аналогично одному из уравнений (5) и описывает собственное движение протона за счет энергии E2. Уравнение (9) описывает субатомные состояния водорода согласно [3]. Рассмотрим эти состояния более подробно и внесем некоторые изменения в отличие от результатов работы [3].
Решение уравнения (9) имеет вид:
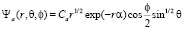. (10)
Энергия связи равна:
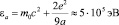. (11)
Здесь боровский радиус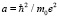 
. Это состояние имеет наибольшую энергию связи и устойчиво к малым взаимным смещениям вероятностных центров протона и электрона [4].
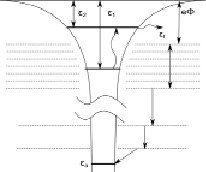
Рис. 2. Энергетические диаграммы атома водорода и титана
Обсуждение экспериментов
Рассмотрим конкретную систему пористый титан насыщенный водородом (это может быть и дейтерий). Будем нагревать эту систему до некоторой температуры, такой, что бы возникли возбужденные атомы водорода, а в спектре теплового излучения атомов водорода будет заметна ультрафиолетовая составляющая с длиной волны λ = 1,215•10–5 cм. Это первая линия серии Лаймана. В этом случае электроны атомов водорода будут туннелировать в зону проводимости титана, см. рис. 2. Работа выхода электрона из титана равна eφ = 3,95 эВ, что больше разницы между вакуумным уровнем водорода и первым возбужденным уровнем. Она равна ε2 = 3,4 эВ. Таким образом, атомы водорода могут частично находиться в ионизованном состоянии. Со дна валентной зоны титана электроны с нулевой энергией поступательного движения могут через множество уровней переходить на субатомный уровень ионизованного водорода, при этом будет выделяться суммарная энергия равная ~ εа в соответствии с (12). Многоуровневые переходы обеспечат «мягкое» излучение рентгеновских квантов. Преимущественный переход электронов на субатомный уровень связан с тем, что энергия Ферми электронов составляет εf = 13,55 эВ и находится ниже основного уровня атома водорода, отсчитанного от вакуумного уровня ε1 = 13,55 эВ.
Субатомы водорода могут приближаться к ядрам других элементов как нейтральные частицы на достаточно близкие расстояния, поскольку протон экранирован электронной оболочкой с большой собственной энергией.
Запишем уравнение движения субатома водорода в поле ядра с Z – номером в таблице Менделеева
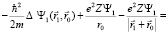
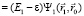. (12)
Здесь r0 – расстояние от центра ядра до вероятностного центра субатома. Будем считать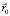 
– параметром задачи и переформируем уравнение (12) в виде:
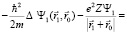
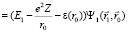. (13)
Это уравнение дает решение для связанных состояний, когда сумма слагаемых в скобках в правой части отрицательна. Несвязанные состояния возникают, когда субатом в сильном электрическом поле ядра распадается на электрон и протон, при положительном значении суммы слагаемых в скобках. Энергия связи будет равна нулю при:
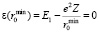(14)
.
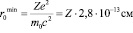Для ядер титана с Z = 22 радиус сближения равен rmin0 ≈ 6,2•10–12 см. Доставка протона в электронной оболочке на такие расстояния к ядрам эквивалентна энергии налетающего протона ~ 500 кэВ и должна заметно повысить вероятность ядерных реакций.
Таким образом, о существовании субатомов водорода в рассматриваемой системе пористый титан + водород можно судить по косвенным признакам: появлению новых элементов и рентгеновскому излучению, которые могут проявиться при нагревании и экспозиции системы во времени. Результаты подобных первых экспериментов описаны в обзоре [5]. С последними экспериментальными работами в этом направлении можно ознакомиться в обзоре [6].
Библиографическая ссылка
Неволин В.К. АТОМЫ ВОДОРОДА НА ОСНОВЕ ГИПОТЕЗЫ ЛУИ ДЕ БРОЙЛЯ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 7-5. – С. 789-791;URL: https://applied-research.ru/ru/article/view?id=9961 (дата обращения: 21.11.2024).