В реальной практической работе приходится иметь дело с результатами измерений, которые в той или иной степени отклоняются от нормального распределения. Поэтому при статическом анализе нового экспериментального материала нередко возникает необходимость оценить степень близости экспериментально наблюдаемого распределения к нормальному.
При современном уровне развития электронно-вычислительной техники получило широкое распространение использование электронных тренажёров, имитирующих лабораторный эксперимент. Для получения квазиэкспериментальных значений измеряемой величины разработчиками используется генератор случайных чисел, соответствующих нормальному распределению. В связи с этим возникает вопрос о близости экспериментального распределения измеряемой физической величины к нормальному распределению.
Оценка близости экспериментального распределения измеряемой физической величины к нормальному распределению проводилась для результатов измерений сопротивлений набора одинаковых по номиналу резисторов.
В работе использовался набор резисторов (100 штук). Сопротивление резисторов измерялось с помощью универсального цифрового вольтметра В7–23. Производство резисторов на заводе – сложный технологический процесс. В результате величина сопротивления резисторов может отличаться от номинала, указанного на каждом экземпляре. Это связано с технологическими погрешностями при изготовлении резисторов. В данной работе для измерения сопротивления используется измерительный прибор, который обеспечивает точность до сотых долей процента относительной погрешности. Таким образом, погрешностью измерений, связанной с измерительным прибором, можно пренебречь по сравнению с отклонениями, полученными в технологическом процессе изготовления резисторов. Результат измерения сопротивлений резисторов приведён в табл. 1.
Таблица 1
Результат измерения сопротивлений ста резисторов
|
473.4 |
484,0 |
485,4 |
486,6 |
488,3 |
|
480.3 |
484,2 |
485,6 |
486,6 |
488,3 |
|
480.9 |
484,3 |
485,6 |
486,6 |
488,4 |
|
481.1 |
484,5 |
485,6 |
486,7 |
488,5 |
|
481.7 |
484,5 |
485,6 |
486,7 |
488,5 |
|
481.8 |
484,5 |
485,7 |
486,8 |
488,6 |
|
482.0 |
484,5 |
485,8 |
486,9 |
488,7 |
|
482.6 |
484,5 |
485,9 |
486,9 |
488,7 |
|
482.8 |
484,7 |
485,9 |
487,0 |
488,7 |
|
482.9 |
484,7 |
486,0 |
487,1 |
489,2 |
|
483.0 |
484,7 |
486,0 |
487,2 |
489,5 |
|
483.3 |
484,8 |
486,1 |
487,2 |
489,6 |
|
483.4 |
484,9 |
486,1 |
487,5 |
490,2 |
|
483.4 |
485,0 |
486,1 |
487,5 |
490,2 |
|
483.5 |
485,0 |
486,4 |
487,5 |
490,3 |
|
483.5 |
485,0 |
486,4 |
487,8 |
490,3 |
|
483.5 |
485,2 |
486,4 |
487,8 |
490,6 |
Оценка степени близости распределения результатов измерений сопротивления набора резисторов к нормальному проводилась на основе χ2–критерия [1].
Для данного набора резисторов рассчитывались среднее арифметическое
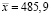Ом
и выборочная дисперисия
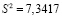Ом2.
Все величины приведены в обозначениях работы [1].
Весь диапазон изменения сопротивлений набора резисторов разбивался на десять интервалов шириной d=2 Ом. Принималось, что верхняя граница интервала не принадлежит ему, и подсчитывалось число попавших в него результатов (табл. 2)
Таблица 2
Обработка результатов определения сопротивлений набора резисторов для расчета χ2-критерия
|
Класс |
Интервал
|
nj |
Интервал
|
Ф(uj) |
Ф(uj+1) |
pj |
Npj |
|
|
1 |
473,4–475,4 |
1 |
––0,94 (n1=12) |
–0,5 |
–0,3264 |
0,1736 |
17,4 |
1,6758 |
|
475,4–477,4 |
0 |
|||||||
|
477,4–479,4 |
0 |
|||||||
|
479,4–481,4 |
3 |
|||||||
|
481,4–483,4 |
8 |
|||||||
|
2 |
484,4–485,4 |
26 |
-0,9-0,20 |
-0,3264 |
-0,0793 |
0,2471 |
24,7 |
0,0684 |
|
3 |
485,4–487,4 |
34 |
-0,20/0,54 |
-0,0793 |
0,2054 |
0,2847 |
28,5 |
1,0614 |
|
4 |
487,4–489,4 |
18 |
0,54/1,28 |
0,2054 |
0,3997 |
0,1943 |
19,4 |
0,1010 |
|
5 |
489,4–491,4 |
9 |
1,28/ ( |
0,3997 |
0,5 |
0,1003 |
10,0 |
0 |
|
491,4–493,4 |
1 |
)Как видно из табл. 2, первые пять интервалов и последние два необходимо объединить, для выполнения условия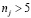 
, поэтому конечное число интервалов составляет k=5.
Сравнив полученное значение χ2-критерия с табличным значением
,
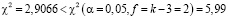получили, что распределение подчиняется нормальному закону.
Определение отклонения распределения случайной величины х от нормального можно оценить с помощью коэффициентов асимметрии Аs и Еk, которые при строго нормальном распределении равны нулю. Если величина As>0, распределение имеет положительную асимметрию (максимум распределения смещен влево), при As < 0 – отрицательную (максимум распределения смещен вправо); если Еk>0 – вершина распределения более заостренная по сравнению с нормальным распределением, а при Еk < 0 – более пологая. Результаты расчета коэффициентов асимметрии и эксцесса для распределения результатов измерений сопротивлений резисторов приведены в табл. 3.
Таблица 3
Расчёт коэффициентов асимметрии и эксцесса для распределения результатов определения сопротивления резисторов
|
Класс |
Интервал
|
|
nj |
|
|
|
|
1 |
479,4–481,4 |
480,4 |
3 |
-5,5 |
-499,125 |
2745,1875 |
|
2 |
481,4–483,4 |
482,4 |
8 |
-3,5 |
-343 |
1200,5 |
|
3 |
484,4–485,4 |
484,4 |
26 |
-1,5 |
-87,75 |
131,625 |
|
4 |
485,4–487,4 |
486,4 |
34 |
0,5 |
4,25 |
2,125 |
|
5 |
487,4–489,4 |
488,4 |
18 |
2,5 |
281,25 |
703,125 |
|
6 |
489,4–491,4 |
490,4 |
9 |
4,5 |
820,125 |
3690,5625 |
|
7 |
491,4–493,4 |
492,4 |
1 |
6,5 |
274,625 |
1785,0625 |
|
Суммы |
450,375 |
10258,1875 |
||||
|
Еk=–0,65 |
||||||
,
.Полученные значения коэффициентов асимметрии и эксцесса для распределения результатов определения сопротивления резисторов показали, что отличие экспериментального распределения результатов измерений сопротивления резисторов от нормального незначимо.
Библиографическая ссылка
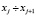
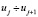
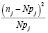
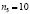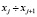
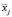
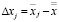
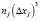
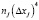
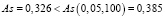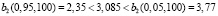Монастырский Л.М. ОЦЕНКА БЛИЗОСТИ ЭКСПЕРИМЕНТАЛЬНОГО РАСПРЕДЕЛЕНИЯ ИЗМЕРЕННОЙ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ К НОРМАЛЬНОМУ РАСПРЕДЕЛЕНИЮ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 11-1. – С. 41-43;URL: https://applied-research.ru/ru/article/view?id=10427 (дата обращения: 23.11.2024).