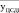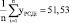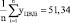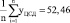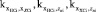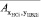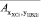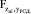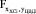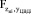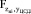Тепловыми электрическими станциями в России производится более 65% электроэнергии. Режимы работы электростанций и отдельных энергоблоков определяются суточным графиком электрических нагрузок энергосистемы [4]. На рис. 1 приведен характерный суточный график для типовой энергосистемы.
Основу энергетических мощностей в энергосистеме России составляют крупные ТЭС и АЭС с конденсационными энергоблоками мощностью 150 - 1200 МВт. Паровые турбины мощностью 200 МВт, установленные на ТЭС, часто работают в переменной части графика электрических нагрузок, поэтому они должны обладать достаточной маневренностью [1].
Современная турбина должна отвечать высоким требованиям безопасности, надежности, экономичности и маневренности.
Наиболее крупной серией блочных конденсационных турбин являются турбины К-200-130. Максимальная наработка ряда турбин превышает 170-180 тыс. часов, число пусков более 1000, парковый ресурс продлен до 220 тыс. часов.
Обязательным требованием ко всем строящимся в настоящее время конденсационным энергоблокам является число пусков, которое должно выдержать оборудование энергоблока за срок службы без повреждений от малоцикловой усталости. Строящиеся энергоблоки мощностью 300 МВт и ниже должны выдерживать не менее 1400 пусков из неостывшего и 6000 - из горячего состояний [2]. Межремонтный период (МРП) увеличивается до 6-8 лет.
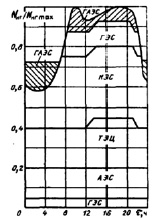
Рис.1. Суточный график нагрузки энергосистемы
В этих условиях актуальным становится установление связи режимных факторов и наработки с повреждаемостью высокотемпературных элементов и ресурсом корпуса ЦВД (цилиндра высокого давления) турбины.
Корреляционно-регрессионный анализ связи режимных факторов и наработки с повреждаемостью высокотемпературных элементов энергоблоков К-200-130
Установим тесноту корреляционной связи на примере статистических данных энергоблоков К-200-130-1,3 Луганской ТЭС [6] (таблицы 1, 2).
Таблица 1
Распределение количества пусков по типам из различных тепловых состояний и наработки для энергоблоков № 11,13-15 ЛТЭС
|
№ наблюдения |
№ блока |
xНСi – число пусков из неостывшего состояния |
xХСi –число пусков из холодного состояния |
zнi – наработка, ч |
|
1 |
11 |
263 |
292 |
280387 |
|
2 |
13 |
250 |
279 |
246901 |
|
3 |
14 |
180 |
259 |
238329 |
|
4 |
15 |
170 |
238 |
246395 |
|
Σ |
863 |
1068 |
1012012 |
|
|
|
|
|
|
, 
, 
Таблица 2
Поврежденность высокотемпературных элементов от малоцикловой усталости, определенная на основании выборок металла для энергоблоков № 11,13-15 ЛТЭС
|
№ наблюдения |
№ блока |
Поврежденность РСД, % |
Поврежденность ЦВД, % |
Поврежденность ЦСД, % |
|
1 |
11 |
81 |
86,85 |
71,52 |
|
2 |
13 |
21,27 |
41,34 |
35,61 |
|
3 |
14 |
47,83 |
34,92 |
50,17 |
|
4 |
15 |
56 |
42,25 |
52,54 |
|
Σ |
206,1 |
205,36 |
209,84 |
|
|
|
|
|
|
, 
, 
где yРСДi - поврежденность РСД (ротора среднего давления); yЦВДi - поврежденность ЦВД (цилиндра высокого давления); yЦСДi – поврежденность ЦСД (цилиндра среднего давления).
Для установления тесноты связи между поврежденностью высокотемпературных элементов от малоцикловой усталости энергоблоков и числом пусков из различных тепловых состояний, а также наработки служат коэффициенты корреляции Пирсона [3],
Результаты расчетов дисперсий Dx, Dz и Dy, выборочных средних квадратичных отклонений σx, σz и σy, выборочных ковариаций и, а также коэффициентов корреляции Пирсона и представлены в виде таблицы 3.
Таблица 3
Показатели корреляции поврежденности высокотемпературных элементов от малоцикловой усталости для энергоблоков № 11, 13-15 ЛТЭС и числа пусков из различных тепловых состояний и наработки энергоблоков
|
Показатели корреляции |
yРСДi – поврежденность РСД |
yЦВДi – поврежденность ЦВД |
yЦСДi – поврежденность ЦСД |
||||||
|
xНСi |
xХСi |
zнi |
xНСi |
xХСi |
zнi |
xНСi |
xХСi |
zнi |
|
|
Dx, Dz |
1694,2 |
418,5 |
261527450 |
1694,2 |
418,5 |
261527450 |
1694,2 |
418,5 |
261527450 |
|
σx, σz |
41,2 |
20,5 |
16171,8 |
41,2 |
20,5 |
16171,8 |
41,2 |
20,5 |
16171,8 |
|
Dy |
454,5 |
428,3 |
163,1 |
||||||
|
σy |
21,3 |
20,7 |
12,8 |
||||||
|
kx, kz |
70,96 |
68,4 |
254102,3 |
584,6 |
290,7 |
333609,9 |
100,4 |
72,6 |
164458,1 |
|
rx, rz |
0,0809 |
0,1568 |
0,7371 |
0,6862 |
0,6866 |
0,9968 |
0,1910 |
0,2778 |
0,7963 |
|
Качество связи |
Слабая |
Слабая |
Высокая |
Заметная |
Заметная |
Весьма высокая |
Слабая |
Слабая |
Высокая |
В таблице 3 дана качественная оценка связи между факторными показателями и результирующими переменными с использованием шкалы Чеддока [6].
Анализ таблицы 3 показывает, что во всех случаях связь прямая, так как r > 0. Между наработкой энергоблоков и поврежденностью от малоцикловой усталости связь высокая для всех высокотемпературных элементов. Между числом пусков из различных тепловых состояний энергоблоков и поврежденностью от малоцикловой усталости она заметна для ЦВД. В остальных случаях связь слабая.
Математическая модель зависимости поврежденности от малоцикловой усталости
Перед построением моделей необходимо проверить факторные показатели на коллинеарность, чтобы исключить из моделей дублирующие факторы. Две переменных явно коллинеарны, если коэффициент интеркорреляции больше 0,7 [6].
Рассчитаем коэффициенты интеркорреляции между факторными показателями по формулам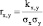 
, 
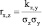и сведем их в таблицу 4.
Таблица 4
Проверка факторов на коллинеарность
|
xНСi и xХСi |
xНСi и zнi |
xХСi и zнi |
|
|
|
801,3 |
477953 |
230100 |
|
|
0,9515 |
0,7180 |
0,6954 |
Анализ таблицы 4 показывает, что коллинеарность факторов xНСi и xХСi, xНСi и zнi, xХСi и zнi сильная, следовательно, мы не можем объединять их в единые модели.
Проведем регрессионный анализ для этого примера и получим следующие однофакторные модели [3].
1. Расчетные значения поврежденности от малоцикловой усталости РСД отдельных энергоблоков, зависящие от наработки этих энергоблоков:
.
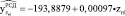2. Расчетные значения поврежденности от малоцикловой усталости ЦВД, зависящие от наработки энергоблоков:
.
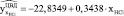3. Расчетные значения поврежденности от малоцикловой усталости ЦСД отдельных от наработки энергоблоков:
.
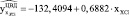4. Расчетные значения поврежденности от малоцикловой усталости ЦВД отдельных энергоблоков, зависящие от числа пусков этих энергоблоков из неостывшего состояния
.
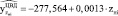5. Расчетные значения поврежденности от малоцикловой усталости ЦВД отдельных энергоблоков, зависящие от числа пусков этих энергоблоков из холодного состояния
.
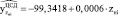Оценим качество составленных моделей, определив для них среднюю ошибку аппроксимации, которая не должна превышать 10-15 %:
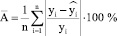(1)
Результаты расчета поместим в таблицу 5.
Таблица 5
Оценка уровня надежности однофакторных регрессионных моделей для поврежденности высокотемпературных элементов, %
|
|
|
|
|
|
|
39,9 |
25,6 |
30,6 |
3,5 |
15,3 |
Анализ данных таблицы 5 показывает, что только четвертая модель имеет высокий уровень надежности, так как средняя ошибка аппроксимации меньше 15 %.
Проверка составленных моделей на адекватность по критерию Фишера дала тот же результат (табл. 6).
Таблица 6
Фактический критерий Фишера
|
|
|
|
|
|
|
2,4 |
1,8 |
1,8 |
305,2 |
3,1 |
Вывод: так как Fф>Fкр, (где Fкр(0,05; 1; 2)=18,51 [5]) для четвертой модели, то она может быть использована для прогнозирования.
Используя четвертую модель, была рассчитана наработка ЦВД, при которой он повреждается на 100% - 290433,8 ч.
На рис. 2 представлены графики зависимости поврежденности ЦВД от малоцикловой усталости от наработки энергоблока, построенные по данным выборки металла и расчета по уравнению регрессии. Анализ графиков показывает, что они мало отличаются друг от друга.
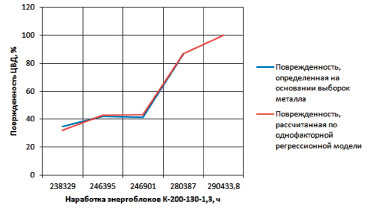
Рис. 2. Зависимость поврежденности ЦВД от малоцикловой усталости от наработки энергоблоков К-200-130-1,3
Проверка влияния различных режимов работы турбины K-200-130-3 на ресурс ЦВД
Исходные данные представлены в таблице 7 [6]. Под предельным временем роста трещины подразумевается время, при котором окружные трещины дорастают до относительной глубины l/δ=0,7, где l – глубина трещины, δ – толщина стенки корпуса ЦВД.
Таблица 7
Ресурс ЦВД на стадии роста трещины стенки корпуса при различных режимах работы турбины K-200-130-3
|
№ наблюдения |
Число пусков из горячего состояния |
Число пусков из неостывшего состояния |
Время предельного роста трещины |
|
1 |
300 |
- |
27,5 |
|
2 |
250 |
50 |
11 |
|
3 |
45 |
20 |
34 |
|
4 |
- |
50 |
32 |
|
5 |
- |
20 |
41,5 |
|
Σ |
595 |
140 |
146 |
Построим двухфакторную регрессионную модель для этого примера.
Расчетное значение предельного времени роста трещины, зависящие от числа пусков этих энергоблоков из горячего и неостывшего состояний.
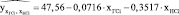
Средняя ошибка аппроксимации данной модели равна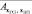 
= 6,7 %.
Модель имеет высокий уровень надежности и пригодна для составления прогнозов.
Используя полученное уравнение регрессии, строим плоскость регрессии (рис.3), показывающую изменение ресурса корпуса ЦВД при изменении числа пусков из горячего и неостывшего состояния.
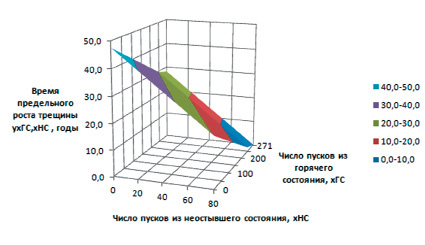
Рис.3. Плоскость уравнения регрессии времени предельного роста трещины от числа пусков из горячего и неостывшего состояния
Выводы
1. Проведены исследования с использованием корреляционно-регрессионного анализа влияния режимных факторов (числа пусков из различных тепловых состояний), а также наработки на показатели надежности (поврежденность высокотемпературных элементов и ресурс корпусов ЦВД).
2. Проверка по критерию Стьюдента показала, что наиболее тесная связь существует между наработкой энергоблока и поврежденностью ЦВД, а также между числом пусков из горячего и неостывшего состояния и ресурсом ЦВД.
3. Расчет средней ошибки аппроксимации и проверка по критерию Фишера показали надежность и адекватность составленных регрессионных моделей, а также их пригодность для составления прогнозов показателей надежности энергоблоков ТЭС.
Библиографическая ссылка
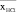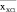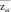
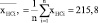
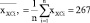
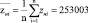
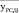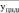Бурденкова Е.Ю., Шевченко Н.Ю., Сошинов А.Г. ПРОГНОЗИРОВАНИЕ ПАРАМЕТРОВ НАДЕЖНОСТИ ПАРОТУРБИННОГО ОБОРУДОВАНИЯ ТЭС ПРИ РАБОТЕ В ПЕРЕМЕННОЙ ЧАСТИ ГРАФИКА ЭЛЕКТРИЧЕСКИХ НАГРУЗОК // Международный журнал прикладных и фундаментальных исследований. 2016. № 12-3. С. 394-399;URL: https://applied-research.ru/ru/article/view?id=10846 (дата обращения: 02.04.2025).