Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Выходец В.И. 1 Никифоров Н.И. 1

---

1 Камышинский технологический институт (филиал) Волгоградского государственного технического университета

Минимальная жёсткость упругого элемента в копирующем инструменте для обработки поверхностным пластическим деформированием должна обеспечивать в случае изменения диаметра соответствующее изменение силы деформирования. Жесткость, рассчитанная по известным методикам, оптимальным образом изменяет усилие обкатки с изменением диаметра заготовки. Но чтобы практически использовать эти методики, необходимо знать функциональную зависимость между усилием дефорирования и диаметром заготовки, которая до сих пор однозначно не установлена. В статье показано, что жёсткость упругого элемента инструмента для ППД имеет линейную зависимость от диаметра обкатываемой детали и предела текучести материала заготовки с коэффициентом пропорциональности, обусловленным усилием обкатки. Определён коэффициент пропорциональности и предложена формула для расчёта жёсткости упругого элемента инструмент для обработки ППД роликами крупных валов.

Статья в формате PDF

442 KB

обкатник

вал

упругий элемент

жёсткость

1. Отений Я.Н., Выходец В.И. Выбор минимальной жёсткости упругого элемента обкатника для обработки крупных валов. Успехи современного естествознания. - 2014.-№12 (часть 2). - С. 99-102.

2. Браславский В.М. Технология обкатки крупных деталей роликами. – 2 изд., М.: «Машиностроение», 1975.–159с.

3. Кудрявцев И.В. Повышение прочности стальных деталей обкаткой. – М.: Машгиз. 1948. – 183с.

4. Шнейдер Ю.С. Чистовая обработка металлов давлением. – М.; - Л.: Машгиз, 1963. – 269с.

В работе [1] показано, что минимальная жёсткость jmin упругого элемента обкатника должна обеспечивать в случае приращения диметра на величину ΔD соответствующее приращение усилия обкатки ΔР. Деформирующий элемент обкатника – ролик воздействует на деталь с одной стороны, поэтому для определения jmin точнее использовать приращение радиуса обрабатываемой детали ΔR.

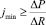(1)

Так как жесткость, рассчитанная по формуле (1), оптимальным образом изменяет усилие обкатки с изменением диаметра заготовки, то при выборе жесткости упругого элемента обкатника знак неравенства в ней можно заменить на знак равенства. Чтобы практически использовать данную формулу, необходимо знать функциональную зависимость между усилием обкатки и диаметром заготовки, которая до сих пор однозначно не установлена. Например, у Н.В. Кудрявцева [3] усилие обкатки пропорционально квадрату диаметра, а у Ю.С. Шнейдера [4] оно связано с радиусом заготовки в степени ¾. Т.е, для разных условий производства, материалов, размеров заготовки и конструктивных элементов обкатника функциональная зависимость Р = f(D) будет разная.

Рассмотрим один из частных случаев, а именно обработку крупных валов роликовым обкатником. Анализ экспериментальных данных, приведённых в работах [1,2] позволяет сделать вывод об увеличении минимальной жёсткости упругого элемента обкатника (далее жёсткости) с увеличением усилия обкатки, диаметра обкатываемой детали и предела текучести материала заготовки. Тогда, принимая во внимание обязательное совпадение размерностей с обеих сторон равенства, можно предложить для расчёта жёсткости следующую формулу:

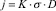(2)

где j – жёсткость, Н/мм; σ – предел текучести материала заготовки, Н/мм2; D – диаметр заготовки, мм; К – коэффициент пропорциональности, значение которого зависит от усилия обкатки.

Рекомендуемые силы обкатки, создающие наклёпанный слой толщиной 0,05 миллиметров, выбираемые в зависимости от диаметра заготовки и предела текучести её материала приведены в источниках [1,2]. На основании этих рекомендаций и с учётом того, что отношение приращения силы к приращению диаметров характеризует жёсткость, составлена таблица 1.

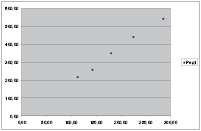
Рис. 1. Зависимость минимальной жёсткости упругого элемента обкатника (ось ординат) от диаметра заготовки при пределе текучести материала заготовки 250 Н/мм2.

По данным этой таблицы были построены две группы графиков (по четыре в группе), представляющих зависимости жесткости от диаметров заготовки (при постоянном пределе текучести материала заготовки) и жёсткости от предела текучести материала заготовки (при постоянном диаметре). Ниже, в качестве примера, приведены два графика.

Обе зависимости блики к линейной, проходящей через начало координат c коэффициентами корреляции Пирсона равными r = 0,998 (для рис. 1) и r = 0,999 (для рис. 2). Методом наименьших квадратов были найдены коэффициенты линейных уравнений и построены теоретические зависимости совместно с исходными (рис.3,4).

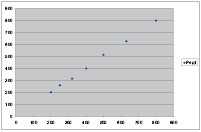
Рис. 2. Зависимость минимальной жёсткости упругого элемента обкатника (ось ординат) от предела текучести материала заготовки при диаметре заготовки 142 мм.

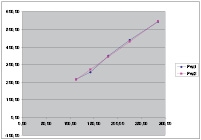
Рис. 3. Зависимость минимальной жёсткости упругого элемента обкатника (ось ординат) от диаметра заготовки при пределе текучести материала заготовки 250 Н/мм2. Ряд 1 – исходная, ряд 2 – теоретическая.

Аналогичный анализ всех графиков обеих групп показал, что жёсткость связана линейной зависимостью с диаметром заготовки и пределом текучести материала заготовки и может быть выражена уравнением (2).

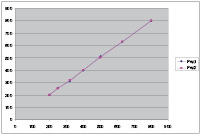
Рис. 4. Зависимость минимальной жёсткости упругого элемента обкатника (ось ординат) от предела текучести материала заготовки при диаметре заготовки 142 мм. Ряд 1 – исходная, ряд 2 – теоретическая.

По восьми теоретическим зависимостям с доверительной вероятностью 0,95 был найден коэффициент пропорциональности в формуле (2): К = 0,00756 ± 0,00024. Искомая жёсткость рекомендуется как минимальная, поэтому выбираем для К верхнее значение диапазона (К = 0,0076+0,00024). Таким образом, расчётная формула для определения минимальной жёсткости упругого элемента обкатника при обработке крупных валов имеет следующий вид.

j = 0,0078• σ • D.

где j – жёсткость упругого элемента обкатника, Н/мм; σ – предел текучести материала заготовки, Н/мм2; D – диаметр заготовки, мм.

Например, жёсткость упругого элемента обкатника при обработке вала диаметром 100 мм, из стали 45 с пределом текучести 360 Н/мм2 , рекомендуется выбирать не менее 281 Н/мм.

Библиографическая ссылка