Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Батраков П.А. 1 Мракин А.Н. 2 Селиванов А.А. 2

---

1 ФГБОУ ВО «Омский государственный технический университет»

2 ФГБОУ ВО «Саратовский государственный технический университет им. Гагарина Ю.А.»

В статье представлены результаты численного анализа процессов теплопереноса и течения реагирующих газов в топках различных профилей топок газотрубных котлов. Расчеты выполнены с использованием программного комплекса ANSYS CFX. Представлены графические результаты исследования в виде переменных, характеризующих тепловые характеристики работы топки и котла в целом. Для выработки рекомендаций по выбору рациональной области максимальных значений тепловых характеристик работы газотрубного котла с топками различного профиля приведены значения температур и зоны их распределения.

Статья в формате PDF

1173 KB

газотрубный котел

топка

интенсификация

тепловосприятие

1. ANSYS CFX-Solver Theory Guide. ANSYS CFX Release 11.0 / ANSYS, Inc. // Southpointe 275 Technology Drive. – Canonsburg: PA 15317, 2006. – 312 p.

2. Kader B.A. Temperature and concentration profiles in fully turbulent boundary layers // International Journal of Heat and Mass Transfer, 1981. 24(9). p. 1541–1544.

3. Батраков П.А. Анализ метода расчета горения в энергетических установках топлива / П.А. Батраков // Россия молодая: передовые технологии – в промышленность. – Омск: Изд-во ОмГТУ, 2015. – №1. – С. 112–114.

4. Белов И.А. Моделирование турбулентных течений / И.А. Белов, С.А. Исаев. – СПб.: Изд. БГТУ, 2001. – 108 с.

5. Госмен А.Д.Численные методы исследования течений вязкой жидкости / А.Д. Госмен, В.М. Пан, А.К. Ранчел, Д.Б. Сполдинг. – М.: Мир, 1972. – 326 с.

6. Зельдович Я.Б. Математическая теория горения и взрыва / Я.Б. Зельдович. – М.: Наука, 1980. – 250 с.

7. Зенкевич О. Конечные элементы и аппроксимация / О. Зенкевич, К. Морган; пер. с англ. – М.: Мир, 1986. – 318 с.

8. Михайлов А.Г. Численное исследование влияния формы топки газотрубного котла на состав продуктов сгорания газообразного топлива / А.Г. Михайлов, П.А. Батраков // Сборник научных трудов SWorld. Материалы международной научно-практической конференции «Перспективные инновации в науке, образовании, производстве и транспорте 2012» – Одесса: КУПРИЕНКО, 2012. – Вып. 2. – Том 8. – С. 94.

9. Михайлов А.Г. Эффективные поверхности теплообмена в топке газотрубного котла: монография / А.Г. Михайлов, П.А. Батраков. – Омск: ОмГТУ, 2014. – 129 с.

10. Оран Э. Численное моделирование реагирующих потоков: Пер. с англ. / Э. Оран, Дж. Борис. – М.: Мир, 1990. – 660 с.

11. Хзмалян Д.М. Теория топочных процессов / Д.М. Хзмалян. – М.: Энергоатомиздат, 1990. – 352 с.

При развитии системы газоснабжения России в малой энергетике все шире применяются газотрубные котлы, которые являются самыми перспективными в сфере автономных теплоисточников, так как они зарекомендовали себя наиболее приемлемыми по сочетанию «цена-качество» как вариант обеспечения жилища теплотой и характеризуются высокой степенью надежности и безопасности, а также простотой в использовании [9]. На данный момент общее количество газотрубных котлов, находящихся в эксплуатации в стране, оценивается в 2,3–2,5 млн. единиц [9].

Процессы горения в топках котлов всегда сопровождаются движением газов – воздуха, газообразного топлива, продуктов сгорания и являются совокупностью взаимообусловленных аэродинамических, тепловых и химических процессов [9, 11].

Течения газов в топках газотрубных котлов, как правило, всегда турбулентные. В процессах горения проблема турбулентности осложнена дополнительными факторами – химическими реакциями и излучением [9]. При этом на теплообмен влияют размеры и конфигурация топочной камеры, способ сжигания и вид топлива, расположение и тип горелок, характеристики среды.

Все это усложняется тем, что к процессу теплопереноса в топках данных котлов предъявляются высокие требования. Для правильной его организации необходимо владеть разноплановой информацией по процессам горения и теплообмена, что заставляет использовать современные программных комплексов. Одним из таких комплексов является ANSYS CFX, позволяющий представить методику расчета, учитывающую процесс горения метана с полным предварительным смешением его c воздухом в горелке, процесс тепломассопереноса в топке, конвективную составляющую, влияние излучения и молекулярную диффузию.

Рассмотрим основные уравнения, которые описывают реагирующую газовую смесь при следующих основных допущениях [1, 5, 6]:

– газовая смесь, заполняющая топочный объем – серое тело;

– теплота от факела к стенке переносится излучением, молекулярной диффузией и конвекцией;

– внутри пограничного слоя давление не изменяется вдоль нормали к контуру тела и равно соответственному давлению на внешней границе пограничного слоя;

– суммарный перенос теплоты на границе раздела газовой смеси – стенка осуществляется за счет конвекции и излучения;

– реагирующий газ CH4=100 %, окислитель – воздух.

1. Неразрывности для всей смеси:

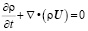, (1)

где ρ – плотность газовой смеси; U – вектор скорости; t – время.

2. Неразрывности для каждого компонента:

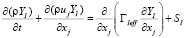,(2)

где SI – скорость образования I-компонента; 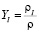– концентрация I-компонента; ρ_I – плотность каждого I-компонента; 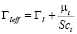– коэффициент диффузии; ГI – коэффициент диффузии для I-компонента; µt – турбулентная составляющая динамической вязкости; 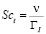– число Шмидта; ν– кинематическая вязкость.

3. Моментов:

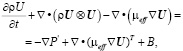(3)

где В – сумма всех сил, действующих на объем газа, μ_eff – эффективная турбулентная вязкость, Р’ – давление.

В формулах (1)–(3) используются следующие обозначения:

,

;

.

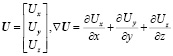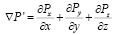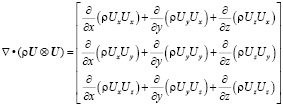4. Энергии и диссипации:

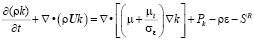, (4)

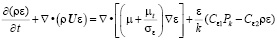, (5)

,

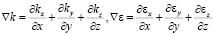где S^R – источниковый член; С_ε1, С_ε2, σ_ε,σ_k – справочные константы, определяемые согласно [4]; Рk – параметр турбулентности, характеризует соотношение между силами вязкости и выталкивающими силами Pkb , рассчитывается с применением [4] по выражению:

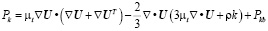. (6)

5. Определение энтальпии

Общая удельная энтальпия htot определяется следующим выражением

h_tot=h+k,

где h – удельная энтальпия неподвижной газовой смеси.

6. Определения вязкости на основе k-ε модели с учетом концепции турбулентной вязкости:

μ_eff= μ + μt, (7)

где μ – динамическая вязкость.

В данной модели предполагается, что турбулентная вязкость связана с турбулентной кинетической энергией и диссипацией через выражение:

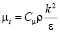, (8)

где Сμ – справочная константа, принимается по [4].

Переменные k и ε являются результатом решения дифференциальных транспортных уравнений для турбулентных кинетической энергии и диссипации.

7. Уравнение состояния Редлиха-Квонга, выглядит следующим образом [4]:

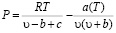, (9)

где υ – удельный объем; a, b и с – константы, зависящие от конкретного вещества.

8. Начальные условия

Принимаются значения всех параметров, входящих в систему уравнений, при времени t=0 и при начальной температуре T=300 K.

9. Граничные условия

Для математического моделирования конкретных течений многокомпонентного реагирующего газа необходимо поставить соответствующие граничные условия [4]:

– условия прилипания на непроницаемой поверхности W

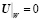. (10)

– задаются условия сложного теплообмена на стенке (рис. 2)

q=qC+qR, (11)

где q – плотность теплового потока через пограничный слой от реагирующей газовой смеси к стенке, qC – плотность конвективного теплового потока, переносимого объемом газа, со стороны реагирующей газовой смеси к пограничному слою, qR – плотность радиационного теплового потока со стороны реагирующей газовой смеси к пограничному слою (определяется методом Монте-Карло при решении системы уравнений (1)–(9)).

Расчетная область представлена на рис. 1.

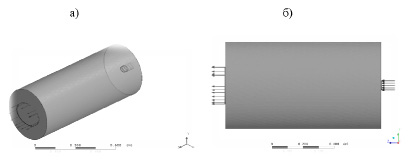
Рис. 1. Расчетные модели топки: а – в объеме, б – вид сбоку

Рис. 2. Расчетная схема сложного теплообмена на стенке

На основании вышеизложенного плотность конвективного теплового потока qС определяется с учетом профиля температуры в пристеночном слое [4]:

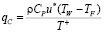, (12)

где CP – массовая изобарная теплоемкость; u* – скорость газовой смеси в пристеночной области; TW – температура стены; TF – температура газовой смеси на границе пристеночного слоя; T+ – безразмерная температура в пристеночном слое [4].

Спектральный тепловой поток излучения qvR, проходя через поверхность с координатой r с единичным вектором n направленным по нормали [2, 8]:

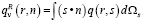, (13)

где 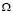– телесный угол.

Интегрируем уравнение переноса по всему телесному углу, тогда дивергенция спектрального теплового потока излучения имеет вид:

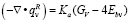, (14)

где Gv – спектральный радиационный параметр; Ka – коэффициент поглощения; Ebv – полное количество энергии, излучаемой абсолютно черным телом.

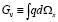. (15)

Полный поток излучения получен интегрированием уравнения для теплового потока излучения по спектру:

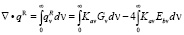.(16)

Результаты данных вычислений подставляются в уравнение энергии в виде величины SR. Далее представлены результаты решения уравнений (1)-(16) [7], реализованных в ANSYS-CFX [1]. Расчетная область топки газотрубного котла приведена на рис. 1, при этом предусматривается изменение формы профиля топки.

Расчетная область представляет собой горизонтально расположенный цилиндр длиной l=1,0 м c эквивалентный диаметр топки dэкв=0,46 м, площадь поперечного сечения топки A=0,17 м2, а площади всех стенок топки 1,74 м2 в которой установлена газовая горелка с предварительной подготовкой топливовоздушной смеси. Изменяемыми величинами при численном исследовании являлась форма профиля топки: прямоугольного, квадратного, круглого, горизонтально и вертикально расположенного эллипса (рис. 3).

Распределение температур вдоль оси топки при различном ее профиле представлено на рис. 4.

На рис. 5 в изометрии изображено распределение температур.

Очевидно, что горение газа сопровождается температурными возмущениями и конвективными явлениями [10]. Область горения совпадает с размерами факела, границей которого является изотерма с максимальной температурой. Внутри топочного пространства процесс горения определяется временем химических процессов [3,9].

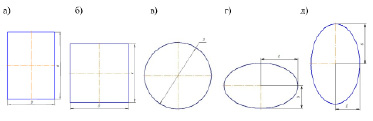
Рис. 3. Геометрические характеристики расчетных моделей: а – прямоугольная форма (a=0,25 м, b=0,18 м – стороны прямоугольника); б – квадратная форма (a=0,21 м – стороны квадрата); в – круг (a=0,46 м – диаметр круга); г – эллипс горизонтальный (a=0,26 м – большая полуось, b=0,2 м – малая полуось); д – эллипс вертикальный (a=0,26 м – большая полуось, b=0,2 м – малая полуось)

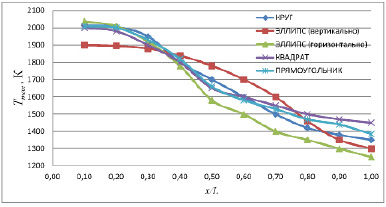
Рис. 4. Распределение температур вдоль оси

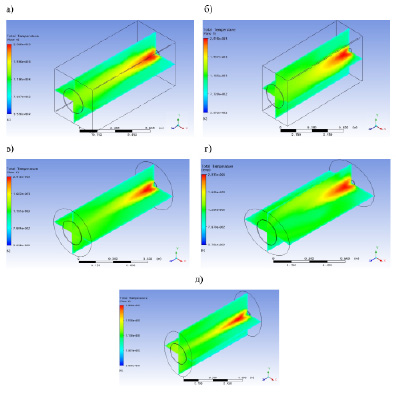
Рис. 5. Распределение температур и скоростей в топке при различных формах её профиля: а – прямоугольная; б – квадратная; в – круглая; г – эллипс горизонтальный; г – эллипс вертикальный

На рассмотрения рисунков 4 и 5 видно как формируется факел по длине топки, а так же как распределяется поле температур. С учетом этих рисунков возможно проанализировать и определить нахождение максимальных температур, а также распределение средних температур по длине топки. При этом в идеале факел должен занимать весь топочный объем и не касаться стенок. В целом наиболее упорядоченное движение газовой смеси соответствует топке с профилем вертикальный эллипс, что способствует формированию зоны максимальных температур относительно равномерно распределенной вдоль оси.

В заключение можно отметить, что изменение формы профиля топки ведет к изменению расположению средних и максимальных температур, так же видно влияние движущегося газа на факел. То есть, можно говорить, что изменение формы профиля топки ведет к изменению тепломассообменого процесса внутри топки.

Библиографическая ссылка