Уравнение Лыкова учитывает, в отличие от уравнения Аллера, конечную скорость распространения возмущения. Оно выведено из принципов необратимой теплодинамики на основе анализа релаксационных процессов, а не исходя из молекулярных представлений капиллярности. В работе [4] для уравнения влагопереноса Лыкова с краевыми условиями первого рода получены априорные оценки в дифференциальной и разностной трактовках. Получены экономичные факторизованные схемы в многомерной области, устойчивость которых доказана с использованием общей теории устойчивости схем. В работе [6] проведено исследование локально-одномерных схем для уравнения теплопроводности с сосредоточенной теплоемкостью. В работе [3] выведена априорная оценка решения уравнения диффузии дробного порядка с сосредоточенной теплоемкостью, построена схема и получена соответствующая априорная оценка в равномерной метрике. В работе [2] был рассмотрен случай многомерной задачи для уравнения диффузии дробного порядка, когда на границе области по каждому направлению помещена сосредоточенная теплоемкость некоторой величины.
Постановка задачи. Устойчивость
В области 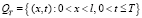 рассматривается задача для уравнения влагопереноса с переменными коэффициентами с сосредоточенной теплоемкостью вида:
рассматривается задача для уравнения влагопереноса с переменными коэффициентами с сосредоточенной теплоемкостью вида:
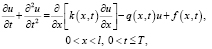 (1)
(1)
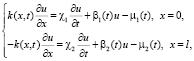 (2)
(2)
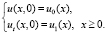 (3)
(3)
Для коэффициентов требуем выполнения условий 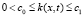 ,
, 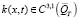 ,
, 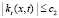 ,
, 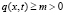 ,
, 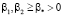 ,
, 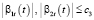 ,
, 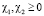 ,
, 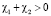 . Здесь
. Здесь 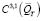 – класс функций, непрерывных вместе со своими частными производными третьего порядка по x и первого порядка по t в
– класс функций, непрерывных вместе со своими частными производными третьего порядка по x и первого порядка по t в 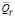 .
.
Доказательство устойчивости решения задачи (1)–(3) проводим с помощью метода энергетических неравенств [5]. Для чего умножаем уравнение (1) скалярно на 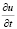 и приходим к энергетическому тождеству:
и приходим к энергетическому тождеству:
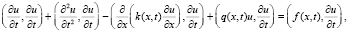 (4)
(4)
где скалярное произведение 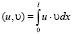 , норма
, норма 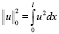 . Для первого и второго скалярных произведений в (4) имеем:
. Для первого и второго скалярных произведений в (4) имеем:
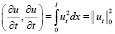 , (5)
, (5)
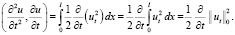 (6)
(6)
Для третьего скалярного произведения в (4) применяем интегрирование по частям. Учитывая условия (2), будем иметь:
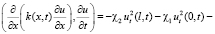
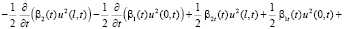
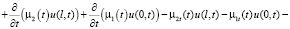
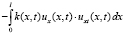 . (7)
. (7)
Используя равенство 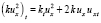 , можем записать
, можем записать 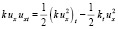 . Тогда для интеграла в (7) будем иметь:
. Тогда для интеграла в (7) будем иметь:
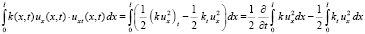 .
.
Теперь (7) с учётом последнего можем переписать:
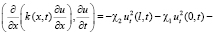

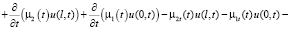
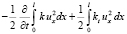 . (8)
. (8)
С учётом условий на k(x, t) и kt(x, t) для интегралов в правой части (8) запишем:
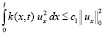 ,
, 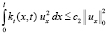 . (9)
. (9)
Для четвёртого интеграла в (4), учитывая условие на q(x, t), можем записать:
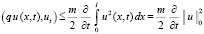 . (10)
. (10)
Для последнего скалярного произведения в тождестве (4) также запишем:
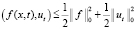 . (11)
. (11)
С учётом (5)–(11) и условий на 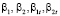 , используя лемму ([1], стр.152), из (4) будем иметь
, используя лемму ([1], стр.152), из (4) будем иметь
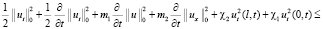
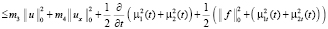 .
.
Учтём условия 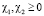 ,
, 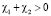 и, пренебрегая положительными слагаемыми, отчего неравенство только усилится, последнее неравенство перепишем:
и, пренебрегая положительными слагаемыми, отчего неравенство только усилится, последнее неравенство перепишем:
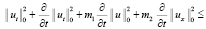
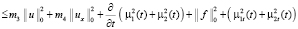 . (12)
. (12)
где m1, m2, m3, m4 – положительные постоянные величины.
Неравенство (12) проинтегрируем теперь по τ в пределах от 0 до и, учитывая начальные условия (3), имеем интегралы:
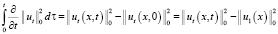 ,
,
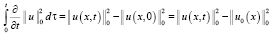 ,
,
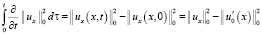 ,
,
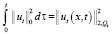 ,
, 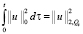 ,
, 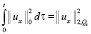 ,
, 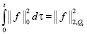 .
.
Учитывая вышеизложенное, перепишем неравенство (12):
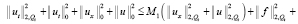
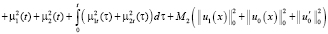
или с учётом того, что 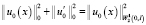 , перепишем неравенство
, перепишем неравенство
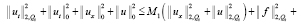
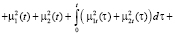
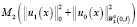 , (13)
, (13)
где M1, M2 – положительные величины. Введем далее обозначение:
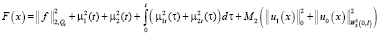 .
.
Тогда неравенство (13), пренебрегая положительными слагаемыми 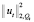 ,
, 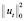 в левой части (отчего неравенство только усилится) перепишем в виде
в левой части (отчего неравенство только усилится) перепишем в виде
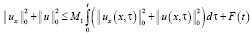 . (14)
. (14)
Введем обозначение: 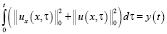 , тогда
, тогда 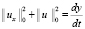 . С учетом принятых обозначений неравенство (14) можем переписать:
. С учетом принятых обозначений неравенство (14) можем переписать:
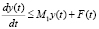 . (15)
. (15)
Применяя известную лемму [1], из неравенства (15) запишем: 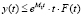 . С учётом последнего и вышесделанных обозначений имеем:
. С учётом последнего и вышесделанных обозначений имеем:
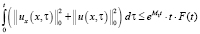 .
.
Из (13), учитывая последнее, получаем неравенство
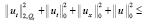
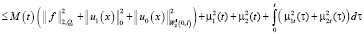 .
.
Поскольку 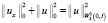 , окончательно получим неравенство
, окончательно получим неравенство
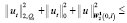
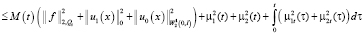 . (16)
. (16)
Здесь положительная величина M(t) зависит от коэффициентов уравнения и размеров области QT. Из априорной оценки (16) заключаем устойчивость решения задачи (1)–(3) по входным данным.
Разностная схема
В 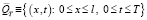 строим сетку
строим сетку 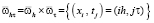 , где
, где 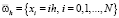 , h – шаг сетки, N – число разбиений;
, h – шаг сетки, N – число разбиений; 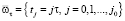 , h – шаг сетки, j0 – число разбиений. Через
, h – шаг сетки, j0 – число разбиений. Через 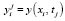 обозначается значение сеточной функции y в узле (xi, tj), определенной на сетке
обозначается значение сеточной функции y в узле (xi, tj), определенной на сетке 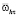 [5]. Дифференциальному уравнению (1) ставится в соответствие параметрическое разностное уравнение вида
[5]. Дифференциальному уравнению (1) ставится в соответствие параметрическое разностное уравнение вида
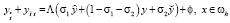 , (17)
, (17)
σ1, σ2 – вещественные параметры, 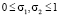 ,
, 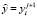 ,
, 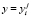 ,
, 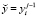 ,
, 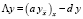 ,
, 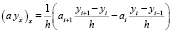 ,
, 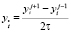 ,
, 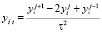 . Разностное уравнение (17) аппроксимирует уравнение (1) с точностью
. Разностное уравнение (17) аппроксимирует уравнение (1) с точностью 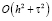 . Следуя [5], получим аппроксимацию краевых условий (2) с точностью
. Следуя [5], получим аппроксимацию краевых условий (2) с точностью 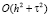 . Для ku' при x = 0 запишем:
. Для ku' при x = 0 запишем:
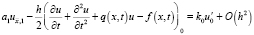 .
.
Тогда для краевого условия (2) при x = 0 имеем
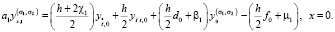 (18)
(18)
Здесь 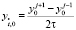 ,
, 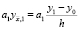 ,
, 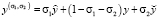 . Также для – ku' в (2) при x = l запишем:
. Также для – ku' в (2) при x = l запишем:
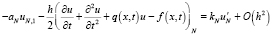 .
.
Тогда аппроксимируется второе граничное условие (2) при x = l в виде
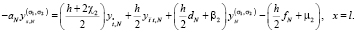 (19)
(19)
Здесь 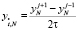 ,
, 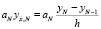 .
.
Первому начальному условию (3) ставим в соответствие разностное условие вида
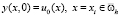 . (20)
. (20)
Второе начальное условие в (3) выражением 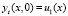 аппроксимируется только с точностью O(τ). Получим аппроксимацию второго порядка по τ. Используя формулу Тейлора, с учётом
аппроксимируется только с точностью O(τ). Получим аппроксимацию второго порядка по τ. Используя формулу Тейлора, с учётом 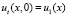 запишем:
запишем:
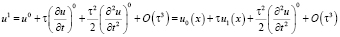 . (21)
. (21)
Выразив 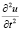 из уравнения (1) и учитывая,
из уравнения (1) и учитывая, 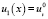 и перенося
и перенося 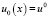 влево и разделив на τ, из (21) получим
влево и разделив на τ, из (21) получим
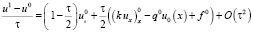 ,
,
откуда
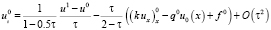 . (22)
. (22)
Итак, получена аппроксимация начального условия 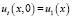 с точностью O(τ2).
с точностью O(τ2).
Таким образом, разностная схема, аппроксимирующая краевую задачу (1)–(3) с точностью 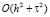 имеет вид
имеет вид
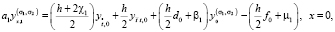 (23)
(23)
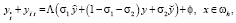 (24)
(24)
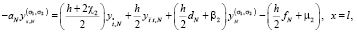 (25)
(25)
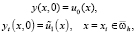 (26)
(26)
где 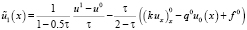 .
.
Для реализации на ЭВМ (23)–(26) приводится к системе уравнений с трёхдиагональной матрицей, которая решается методом прогонки на каждом временном слое.
Библиографическая ссылка
Нахушева Ф.М., Куважукова Р.Х., Максидова З.Т. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВЛАГОПЕРЕНОСА С СОСРЕДОТОЧЕННОЙ ТЕПЛОЁМКОСТЬЮ // Международный журнал прикладных и фундаментальных исследований. 2017. № 7-1. С. 48-53;URL: https://applied-research.ru/ru/article/view?id=11689 (дата обращения: 11.02.2026).

