Исследование кинематики, динамики и управление платформой Стюарта (ПС) имеется во многих публикациях, в частности [1–3]. Была выбрана конструкция рычажной ПС с шестью степенями свободы и управляемой шестью сервоприводами.
Целью настоящей работы является проектирование, изготовление макета, создание системы управления ПС, имеющей простую конструкцию и низкую стоимость.
Материалы и методы исследования
На рис. 1 показана трехмерная модель ПС, созданная в компьютерной системе Inventor.
Как видно из рисунка, размеры ПС проектировались с учетом размеров сервопривода марки SM-S8330M. На двигатель надевается рычаг. Стержень с двумя сферическими шарнирами на концах соединяется снизу с рычагом, сверху с платформой. Основные детали ПС были изготовлены из пластмассы на лазерном станке с использованием компьютерных моделей.
Результаты исследования и их обсуждение
Для управления сервоприводами ПС была рассмотрена обратная кинематика ПС, поскольку прямая кинематика дает 40 возможных решений [1]. Сама платформа Стюарта состоит из подвижной платформы и основания, соединенных шестью стержнями со сферическими шарнирами на концах с шестью рычагами.

Рис. 1. Трехмерная модель ПС, созданная в компьютерной системе Inventor
Основание имеет систему координат с осями х, у, z. Платформа имеет свою подвижную систему координат х’, у’, z’. Начало координат платформы определяется с помощью 3 поступательных перемещений вдоль осей х, у, z относительно основания. Три угла поворота вокруг осей определяют ориентацию платформы по отношению к основанию: поворот на угол ψ вокруг оси z, поворот на угол q вокруг оси у, поворот на угол j вокруг оси х.
Рассмотрим поворот относительно оси z на угол ψ. Тогда матрица вращения Rz(y) имеет вид
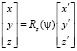
и 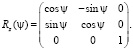
Аналогично, имеем матрицу вращения для поворота вокруг оси у на угол q
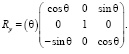
Для третьего поворота на угол j вокруг оси х имеем
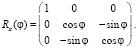
Полная матрица вращения платформы по отношению к основанию затем определяется по формуле
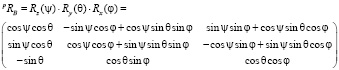
Теперь рассмотрим i-ый стержень платформы Стюарта.
Координаты qi точки cсоединения верхней точки Pi относительно системы координат основания задаются уравнением
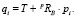
Здесь вектор T описывает линейное перемещение начала координат платформы по отношению к системе координат основания, pi – является вектором, определяющим координаты точки соединения Pi относительно системы координат платформы.
Аналогичным образом длина i-ого стержня задается в виде
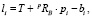
где bi – вектор, определяющий координаты нижней точки Bi соединения стержня. С помощью 6 уравнений определяют длины 6 стержней, таким образом определяется положение и ориентация платформы.
На рис. 2 также показан сервопривод с центром вращения в точке Вi. Необходимо определить угол поворота вала сервопривода. При нахождении формулы использовались следующие обозначения: а – длина рычага сервопривода, Аi – точки соединения рычага с нижней точкой стержня i-го сервопривода с координатами а = [xa, ya, za] в системе координат основания, Вi – точки вращения центра рычага сервопривода с координатами b = [xb, yb, zb] в системе основания, Pi – точки соединения верхнего шарнира стержня с платформой, с координатами р = [xр, yр, zр] в системе координат платформы, S – длина стержня, li = длина i-ого стержня, α – угол между рычагом сервопривода и горизонталью, β – угол между рычагом сервопривода и осью х.
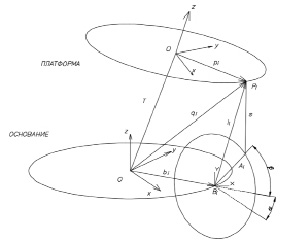
Рис. 2. Системы координат основания и платформы
Для четных и нечетных стержней можно записать
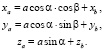
Рассмотрение геометрии рис. 2 приводит к уравнению:
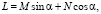
где
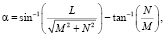
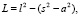
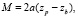
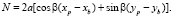
Для определения положения, с которого начинается движение, выберем положение, когда платформа находится на высоте h0 над основанием и нет поступательного или вращательного движений (рычаг и стержни находятся под прямым углом друг к другу). Тогда
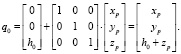
В этом случае
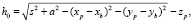
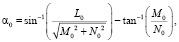
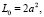
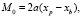
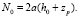
Для спроектированной трехмерной модели был изготовлен макет ПС из пластика и металлических деталей. Для управления сервоприводами использовался микроконтроллер Arduino. Размеры деталей: а = 58 мм, S = 184 мм, bi = 600, 00, 1800, 1200, –600, –1200, углы точек закрепления шарниров на платформе с осью х – gр = 334,20, 85,80, 94,30, 205,80, 214,20, 325,80, углы точек закрепления сервопривода на основании с осью х – gb = 7,60, 52,40, 127,60, 172,40, 247,60, 292,40.

Рис. 3. Макет платформы Стюарта
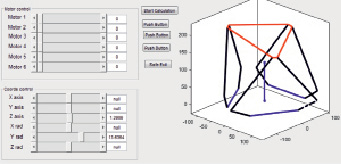
Рис. 4. Окно с ползунками управления и анимацией движения ПС
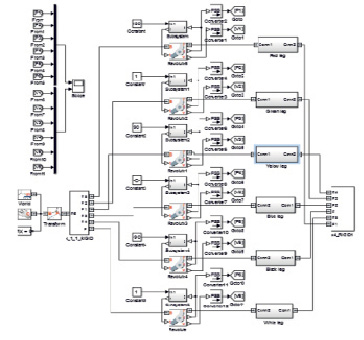
Рис. 5. Модель ПС в системе Matlab Simulink
Для проверки работоспособности изготовленного макета ПС, создания анимации движения и для управления сервоприводами была разработана программа в системе Matlab. Управление сервоприводами осуществлялось путем перемещения ползунков, настроенных на три перемещения и три вращения центра тяжести платформы в специальном окне (рис. 3). Это окно имеет также управление ползунками каждого из шести двигателей и анимацию движения платформы, зависящую от перемещения ползунков. Кроме того, в окне имеется кнопка для установки начального положения ПС. Для установления связи программы написанной в системе Matlab к системе были подключены модули управления микроконтроллером Arduino. Таким образом, перемещение ползунка соответствующей координаты дает нам перемещение как на трехмерной анимации в окне, так и в самом макете ПС.
Диапазон движения платформы вдоль х, у и z осей составляет примерно ± 18, ± 19 и ± 16 мм, повороты вокруг осей х, у и z составляют около ± 60, ± 60 а также ± 70 соответственно.
Точность платформы ограничена в основном разрешающей способностью сервоприводов. Скорость работы сервоприводов составляет 0,22 сек 60 °, крутящий момент двигателя – 30 кг/cм.
С помощью встраиваемой библиотеки SimMechanics в систему Matlab Simulink и трехмерной модели платформы Стюарта получили блоки, которые с высокой точностью описывают твердые тела с учетом их массово-инерционных характеристик, расположения, степеней свободы и связей между ними, а также измерять параметры их движения под действием сил и моментов в различных системах координат.
С помощью этих блоков смоделировали механическую модель платформы Стюарта в системе Matlab Simulink.
Также была написана программа в системе Matlab для управления моделью платформы Стюарта. Каждый ползунок в программе отвечает за один из шести двигателей. Кнопка DEFAULT отвечает за сброс значений ползунков, а кнопка Scope выводит графики изменения положения и скорости каждой ноги платформы Стюарта.
Выводы
Создан макет платформы Стюарта. С использованием уравнений обратной кинематики, системы Matlab и микроконтроллера Arduino разработана система управления платформой Стюарта. Динамическую модель платформы Стюарта получили с помощью встраиваемой библиотеки SimMechanics в системе Matlab Simulink и трехмерной модели платформы Стюарта.
Библиографическая ссылка
Сейдахмет А.Ж., Абдураимов А.Е., Камал А.Н. ИСПОЛЬЗОВАНИЕ ОБРАТНОЙ КИНЕМАТИКИ И СИСТЕМЫ MATLAB ДЛЯ УПРАВЛЕНИЯ РЫЧАЖНОЙ ПЛАТФОРМОЙ СТЮАРТА // Международный журнал прикладных и фундаментальных исследований. 2017. № 8-2. С. 216-220;URL: https://applied-research.ru/ru/article/view?id=11788 (дата обращения: 27.02.2026).
DOI: https://doi.org/10.17513/mjpfi.11788

