Металло-интерметаллидные слоистые композиционные материалы (МИСКМ) – перспективные материалы для авиакосмической отрасли и ряда других технических приложений [1–3]. Среди возможных МИСКМ выделяются системы титан-алюминий. В системе Ti-Al формирование интерметаллидного триалюминид титана Al3Ti является термодинамически предпочтительным перед другими алюминидами титана – AlTi, AlTi3. По сравнению с другими алюминидами титана у триалюминида титана ниже плотность (3,3 г/см3), выше модуль Юнга (216 ГПа) [1]. Интерметаллиды в целом обладают высокой твердостью и жесткостью, что означает высокий предел прочности при сжатии. Такое свойство интерметаллидов обусловлено высокой прочностью межатомной связи. Обратной стороной данного свойства интерметаллидов является их хрупкий характер разрушения. В частности, интерметаллид Al3Ti имеет низкую трещиностойкость ~2 МПа м1/2 [1]. Однако слоистый металло-интерметаллидный композит Ti-Al3Ti, в котором друг за другом расположены слои титанового сплава и триалюминида титана, обладает повышенными удельными прочностными характеристиками, сравнимыми со сталью и керамическими материалами [1].
В исследованиях поведения МИСКМ при динамическом нагружении преобладают экспериментальные работы [4]. Однако в ходе быстропротекающего процесса сложно регистрировать динамику самого процесса, что затрудняет выявление механизмов разрушения. В то же время численное моделирование позволяет исследовать особенности деформирования, а также разрушения взаимодействующих тел во времени [5–7].
В данной работе выполнено численное моделирование деформирования и разрушения многослойных композитов титан – триалюминид титана при высокоскоростном ударе. В расчетах варьировались толщины слоев интерметаллид/металл с целью оценки прочностных характеристик композита и поиска оптимального соотношения толщин слоев с точки зрения стойкости композита к высокоскоростному удару. Проведены сравнения многослойных композитов с монолитными преградами из интерметаллида и титанового сплава.
Постановка задачи
Рассматриваемый процесс имеет нестационарный адиабатический характер. При его описании используется упругопластическая модель среды. Система основных уравнений включает уравнения сохранения массы, импульса, энергии [6]. Уравнение состояния (УРС) типа Ми – Грюнайзена (с выделением «холодной» и «тепловой» частей) определяет давление в материале в зависимости от удельных объема и внутренней энергии. Подбор коэффициентов в УРС проводится на основе констант ударной адиабаты Гюгонио. Определяющие соотношения связывают компоненты девиатора напряжений и компоненты тензора скоростей деформаций. При этом используется производная по Яуманну. Пластическое течение описывается с использованием условия текучести Мизеса. Учитывается влияние температуры и уровня поврежденности материала на прочностные характеристики среды (модуль сдвига и динамический предел текучести).
Для моделирования разрушения слоев из титанового сплава при растягивающих нагрузках используется кинетическая модель разрушения активного типа [6]. Для описания разрушения интерметаллида используется модель хрупкого разрушения [8].
Указанные выше модели работают в областях сжатия и растяжения. В областях интенсивного пластического деформирования применяется модель разрушения эрозионного типа [9]. В качестве критерия разрушения используется критическое значение удельной энергии сдвиговых деформаций. Удельная энергия сдвиговых деформаций Esh вычисляется по формуле
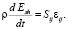 (1)
(1)
Критерий хрупкого разрушения полагается зависящим от прочностных характеристик материала и начальной скорости удара:
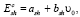 (2)
(2)
где ash, bsh – константы модели. Когда выполняется условие
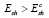 (3)
(3)
в расчетном конечном элементе, этот элемент полагается разрушенным и удаляется из расчета. Соседние расчетные узлы корректируются с учетом законов сохранения. Корректировка сводится к удалению масс узлов разрушенного элемента. В ходе такой корректировки масса какого-либо узла может стать равной нулю, в этом случае данный узел считается разрушенным и удаляется из расчета.
Такая процедура удаления массы из масс узлов соответствует закону сохранения массы. Физически процесс эрозионного разрушения означает отделение частиц от рассматриваемого образца в процессе нагружения и унос этих частиц в виде разрушенного материала. Такой процесс сопровождается уменьшением массы образца. При численном моделировании с использованием описанной выше модели эрозионного разрушения разрушенные элементы удаляются из конечно-элементной модели, что, в соответствии с физикой процесса эрозионного разрушения, сопровождается уменьшением массы рассматриваемого образца. Поэтому в соответствии с законом сохранения массы масса расчетных элементов также должна быть уменьшена на величину массы разрушенного материала.
Рассматривается задача взаимодействия ударника из вольфрамового сплава, имеющего коническую форму головной части, с многослойной композиционной преградой при высокоскоростном ударе. Задача решается в осесимметричной постановке. Для решения задачи используется модифицированный метод конечных элементов без глобальной матрицы жесткости, предназначенный для решения задач высокоскоростного нагружения [10].
Численные результаты
Численно моделировался процесс взаимодействия ударника из вольфрамового сплава 93W-7FeCo с многослойной преградой. Диаметр ударника равен 6,15 мм, длина 23 мм. Угол раствора конуса ударника 500, начальная скорость удара 900 м/с. Преграда состояла из 17 композиционных слоев, каждый из которых состоял из слоя интерметаллида Al3Ti и слоя титанового сплава ВТ6. Толщины слоев титанового сплава и интерметаллида варьировались при общей неизменной толщине композиционного слоя, равной 1,17 мм. Толщина композиционной преграды составила 19,89 мм. Проведены также сравнения с монолитными интерметаллидной преградой и преградой из титанового сплава. Характеристики материалов приведены в [6].
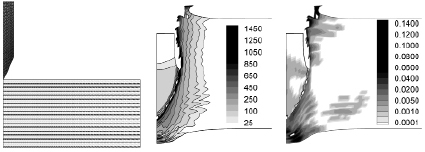
Рис. 1, а, иллюстрирует расчетную конечно-элементную сетку. В преграде реализовано неравномерное разбиение вдоль радиуса с увеличением размера элементов по мере удаления от области взаимодействия. В рассматриваемом случае толщины слоев композиционного слоя составили 0,94 мм – интерметаллид Al3Ti, 0,23 мм – титановый сплав ВТ6, что соответствует варианту «ж» в таблице. Рис. 1, б, в, представляют результаты расчета к моменту времени 60 мкс после начала взаимодействия, при этом приведена область взаимодействия без периферийной части преграды. На рис. 1, б приведены распределения удельной энергии сдвиговых деформаций начиная с 25 кДж/кг с интервалом от 75 до 200 кДж/кг; на рис. 1, в – удельного объема микроповреждений начиная с 0,0001 см3/г с интервалом до 0,02 см3/г. Видно, что ударник в ходе процесса деформируется и срабатывается, слоистая преграда выдерживает удар, хотя и значительно разрушается. На тыльной поверхности преграды формируется выпуклость, но сквозного пробития преграды не наблюдается.
Под действием ударника более половины слоев преграды разрушаются в области взаимодействия. Слои интерметаллида и титанового сплава разрушаются по разным механизмам. В титановом сплаве, в сравнении с интерметаллидом, в большей степени накапливается энергия сдвиговых деформаций (Еsh) вследствие пластических деформаций слоя и в значительно меньшей – удельный объем микроповреждений (Vf), что наглядно иллюстрирует рис. 1, в. Титановые слои таким образом препятствуют распространению магистральных трещин, формирующихся в хрупких интерметаллидных слоях под действием как сжимающих (в области удара перед ударником), так и растягивающих напряжений в остальных областях преграды. Области с максимальными значениями Еsh наблюдаются вдоль контактных поверхностей взаимодействующих тел. Области с максимальными значениями Vf наблюдаются около свободных поверхностей преграды (лицевой и тыльной), что обусловлено действием отраженных волн разгрузки, а также по ходу движения ударника.
На рис. 2 приведены распределения удельного объема микроповреждений в радиальном сечении во взаимодействующих телах в момент времени 60 мкс. Уровни Vf аналогичны рис. 1, в.
а б в
Рис. 1. Радиальное сечение ударника и многослойной преграды, вариант «ж» в таблице: а – расчетная конечно-элементная сетка в начальный момент времени; б, в – поля удельной энергии сдвиговых деформаций (кДж/кг) и удельного объема микроповреждений (см3/г) во взаимодействующих телах в момент времени 60 мкс
Результаты моделирования для слоев МИСКМ различной толщины
|
Толщина слоя, мм |
Поверхностная плотность, г/см2 |
Глубина проникания, мм |
Средняя скорость, м/с |
||||
|
Al3Ti |
ВТ6 |
40 мкс |
60 мкс |
40 мкс |
60 мкс |
||
|
а |
1,04 |
0,13 |
6,81 |
22,9 |
– |
440 |
– |
|
б |
0,70 |
0,47 |
7,52 |
21,9 |
26,4 |
410 |
220 |
|
в |
0,47 |
0,70 |
7,99 |
23,0 |
28,7 |
430 |
250 |
|
г |
0,23 |
0,94 |
8,49 |
24,2 |
– |
470 |
– |
|
д |
0 |
1,17 |
8,97 |
18,7 |
20,9 |
200 |
50 |
|
е |
1,17 |
0 |
6,54 |
21,1 |
25,4 |
350 |
150 |
|
ж |
0,94 |
0,23 |
7,02 |
17,0 |
18,5 |
150 |
30 |
а б в

г д е
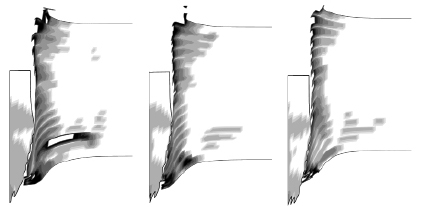
Рис. 2. Удельный объем микроповреждений в радиальном сечении взаимодействующих телах в момент времени 60 мкс. Параметры вариантов а – е представлены в таблице
Указанные варианты отличаются соотношением толщин слоев интерметаллида и титанового сплава, при этом в варианте «а» толщина интерметаллидного слоя выше рассмотренного ранее (вариант «ж»), а в вариантах «б–г» – ниже. Для сравнения приведены результаты для монолитных преград из ВТ6 (рис. 2, д) и Al3Ti (рис. 2, е). Все перечисленные варианты демонстрируют худшие результаты по сравнению с ранее рассмотренным вариантом. Этот же вывод подтверждают результаты расчетов, приведенные в таблице, где даны глубины внедрения и средние скорости ударника в моменты времени 40 и 60 мкс. Причем для некоторых вариантов не приводятся значения для момента времени 60 мкс, так как результат взаимодействия – сквозное пробитие – определяется раньше.
Заключение
Результаты численного моделирования деформирования и разрушения многослойных композитов титан – триалюминид титана при высокоскоростном ударе показывают, что композиционная преграда с отношением слоев триалюминид титана / титановый сплав ≈ 4 демонстрирует отсутствие пробития. Преграда из титанового сплава также выдерживает удар. Остальные композиционные преграды с соотношением слоев как выше 4, так и ниже, так же как и преграда целиком из интерметаллида, демонстрируют пробитие преграды.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 16-08-00037).
Библиографическая ссылка
Зелепугин А.С., Зелепугин С.А. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ РАЗРУШЕНИЯ МНОГОСЛОЙНЫХ КОМПОЗИТОВ ТИТАН – ТРИАЛЮМИНИД ТИТАНА ПРИ ВЫСОКОСКОРОСТНОМ УДАРЕ // Международный журнал прикладных и фундаментальных исследований. 2017. № 11-2. С. 194-198;URL: https://applied-research.ru/ru/article/view?id=11997 (дата обращения: 13.03.2026).
DOI: https://doi.org/10.17513/mjpfi.11997

