Круговые пластины широко применяются в различных отраслях техники в качестве рабочих элементов в нефтеперерабатывающей промышленности, авиастроении, в гражданском строительстве и др.
Определению собственных частот колебаний круговых пластин, как свободных так и покоящихся на упругом основании типа Винклера, посвящён ряд работ [1–4]. Только для статических задач об изгибе прямоугольных пластинок, лежащих на упругом основании с переменным коэффициентом постели, известны решения. В статье [5] расчёт таких пластинок ведется методом конечных элементов, а в [6] – методом Галёркина.
В данной работе рассматриваются свободные колебания круглой пластины, подвешенной различными способами с Винклеровым основанием. Очевидно, вид подвески будет сказываться на частоте колебаний. На практике опора пластины может оказаться отличной от планируемой, и поэтому необходимо знание, как она влияет на частоту колебаний. В работе [7–10] исследованы симметричные поперечные колебания металлополимерной трехслойной круговой пластины, связанной с упругим основанием, при тепловом ударе. Для внешних слоев принимаются гипотезы Кирхгофа, в легком заполнителе деформированная нормаль прямолинейна и несжимаема по толщине. Получены аналитические решения, проведен их численный анализ.
В работе [11] представлено решение уравнения собственных колебаний лежащей на деформируемом основании трансверсально-изотропной пластины, один край которой жестко закреплен, а три других шарнирно оперты. Задача решается методом декомпозиций, получено частотное уравнение для определения собственных поперечных колебаний пластины.
В работе [12] рассматриваются задачи свободных колебаний круглых пластин при различных вариантах подвески.
При колебаниях пластины на его опоры действуют значительные усилия, в результате в которых они деформируются, и естественно, это влияет на частоту колебания пластины.
Цель работы: исследование колебаний пластины в случае податливости опоры. Выяснить особенности колебаний при наличии основания Винклера, а именно в одном случае решение представляется при помощи функций Бесселя, в другом – при помощи функций Кельвина.
Уравнение колебаний пластины имеет вид [13, с. 678]:
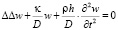
здесь подставляя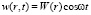 
, тогда получим
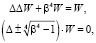(1)
где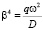 
, β – функции частоты; 
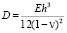– цилиндрическая жёсткость пластины, Е – модуль упругости материала пластинки; 
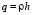– масса пластины, h – толщина пластинки, ρ – плотность материала; k – сопротивление грунта оседанию, когда оседание, отнесённое к единице поверхности, равно единице; r0 – радиус пластины, ω – частота колебаний, ν – коэффициент Пуассона, Δ – оператор Лапласа.
Решение уравнения (1) имеет вид:
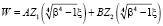, (1/)
где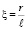 
.
Если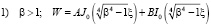 
. (2)
Если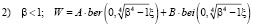 
. (2/)
В дальнейшем понадобятся производные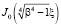 
, 
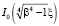Бесселевых и 
, 
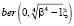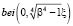Кельвин функций.
Пластина шарнирно закреплена по контуру и упруго опирается (рис. 1).
Рис. 1. Пластина шарнирно закреплена по контуру и упруго опирается
Условие шарнирного закрепления имеет вид
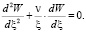(3)
Условие упругого опирания при r = ξ
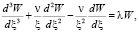(4)
здесь λ – жесткость постели Винклера.
Подставляя (2) в (3) и (4), получаем, учитывая
;
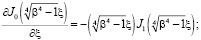
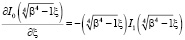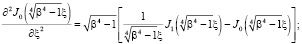
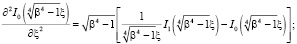
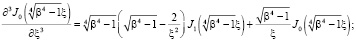
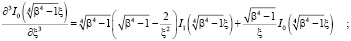
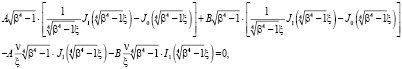(5)
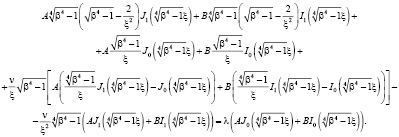(6)
Получим из (5)
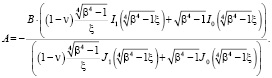(7)
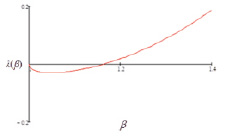
Рис. 2. График I функции жесткости постели Винклера в зависимости от частоты (то есть обратное решение)
Подставляя (7) в (6), имеем
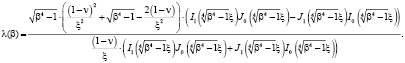(8)
На рис. 2 представлен график функции λ(β)
Если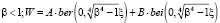 
.
Подставляя (2/) в (3) и (4), получаем, учитывая
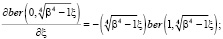
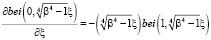
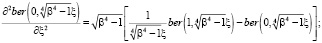
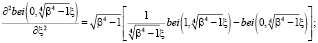
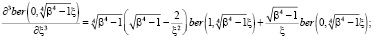
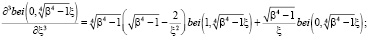
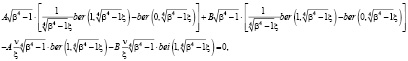(9)
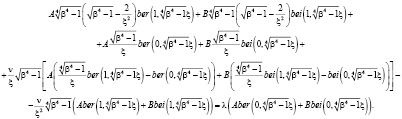(10)
Получим из (9)
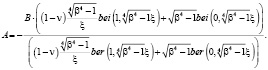(11)
Подставляя (11) в (10), имеем
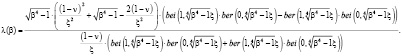(12)
На рис. 3 представлен график функции λ(β).
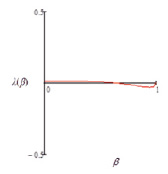
Рис. 3. График II функции жесткости постели Винклера в зависимости от частоты (то есть обратное решение)
Представлены свободные колебания для различных возможных случаев закрепления круглых пластин.
Заключение
Впервые изучается влияние податливости опоры на колебания упругих систем, в частности, на свободные колебания пластины. Притом при наличии упругих оснований выявлено интересное явление: характер колебаний качественно зависит от соотношения параметров постели Винклера и упругости опоры. Учёт изученных явлений представляет интерес для применения на практике.
Следует учитывать, что постель Винклера ведёт к качественно изменяющемуся состоянию колебаний, характеризующемуся выражению решений различными классами функции, а именно Бесселевыми и функцией Кельвина.
Библиографическая ссылка
Агаларов Дж.Г., Мамедова Г.А. КОЛЕБАНИЯ ПЛАСТИНЫ, ШАРНИРНО ЗАКРЕПЛЁННОЙ И УПРУГО ПОДВЕШЕННОЙ НА ВИНКЛЕРОВОМ ОСНОВАНИИ // Международный журнал прикладных и фундаментальных исследований. – 2018. – № 7. – С. 48-53;URL: https://applied-research.ru/ru/article/view?id=12328 (дата обращения: 03.12.2024).