Статья посвящена исследованию пространства Лоренца в терминах теории тригонометрических рядов Фурье и тригонометрических наилучших приближений. В данной статье рассмотрена связь между тригонометрическими наилучшими приближениями в пространстве Лоренца в разных метриках. Связь между наилучшими приближениями в пространстве Lp[0; 2π] была установлена А.А. Конюшковым, П.Л. Ульяновым и М.Ф. Тиманом [1, c. 86–92].
Эти вопросы также доказаны Е.С. Смаиловым [2, c. 140–151].
Пусть f(x) – измеримая на [0, 2π] в смысле Лебега функция, f*(x) – невозрастающая перестановка функции 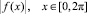 [3, с. 104–131]. Пусть
[3, с. 104–131]. Пусть 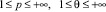 . Будем говорить, что функция f(x) принадлежит пространству Лоренца Lpθ, если
. Будем говорить, что функция f(x) принадлежит пространству Лоренца Lpθ, если
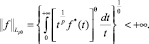
Пусть Tn(x) – тригонометрический многочлен порядка не выше, чем n∈N, f∈Lpθ[0; 2π], 1 < p < +?+∞, 1 ≤ θ ≤ +∞. Наилучшим приближением функции f в пространстве Lpθ[0; 2π] посредством тригонометрических полиномов порядка не выше, чем n, назовем величину
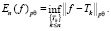
Пусть 1 ≤ p < ∞, 1 ≤ θ < ∞. Пространства Лоренца Lpθ определяются следующим образом
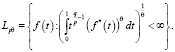
Если θ < ∞,,
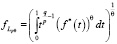 .
.
Если θ = ∞,
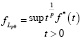 ,
,
где f*(t) – невозрастающая перестановка функций 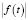 .
.
Пространства Лоренца Lpθ являются более тонкой шкалой пространств, чем шкала пространств Лебега, и имеют большое применение в теории рядов Фурье, в дифференциальных уравнениях, в теории функциональных пространств.
Пусть 1 ≤ p < ?. В случае, когда p = θ, пространства Лоренца Lpθ совпадают с пространствами Лебега Lp [4, с. 4–16].
Основными свойствами пространства Лоренца являются зависимости ее параметров, т.е. имеют место следующие свойства:
1. Если 1 ≤ p < ∞, 1 ≤ θ < θ1 < ∞, тогда имеет место вложение
Lpθ↪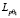
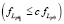 .
.
2. Для любого ε > 0 иммет место следующее вложение пространств
Lpθ↪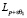 .
.
Далее приведем необходимые вспомогательные предложения.
Лемма 1. Пусть 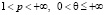 ,
, 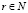 и Tn(x) – произвольный тригонометрический многочлен. Тогда справедливо следующее неравенство, называемое неравенством Бернштейна:
и Tn(x) – произвольный тригонометрический многочлен. Тогда справедливо следующее неравенство, называемое неравенством Бернштейна:
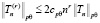 ,
,
где 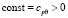 не зависит от Tn.
не зависит от Tn.
Лемма 2. Пусть 1 < p < q < +∞, 0 < ? < +∞ и 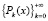 – произвольная последовательность тригонометрических многочленов. Тогда
– произвольная последовательность тригонометрических многочленов. Тогда 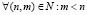 справедливо следующее неравенство:
справедливо следующее неравенство:
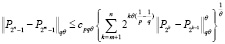 ,
,
где 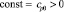 не зависит от
не зависит от 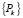 и
и 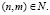
Лемма 3. Пусть 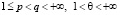 ,
, 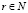 и f∈Lpθ[0; 2π].
и f∈Lpθ[0; 2π].
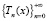 – последовательность ее тригонометрических многочленов наилучшего приближения. Тогда
– последовательность ее тригонометрических многочленов наилучшего приближения. Тогда 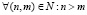 справедливо неравенство
справедливо неравенство
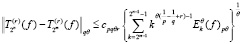 ,
,
где 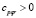 не зависит от f и n, m.
не зависит от f и n, m.
Применяя методику, предложенную в [5, с. 305–309], доработанную с учетом особенности пространства Лоренца, доказывается следующая вспомогательная теорема, которая сама по себе является важным утверждением. Для тригонометрических рядов также рассмотрено в [6, с. 213–223].
Теорема 1. Пусть 1 < p < q < +∞, 1 < θ < +∞ и
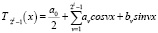 ,
, 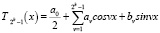 ,
,
тогда имеет место следующее неравенство:
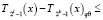
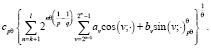
Теорема 2. Пусть 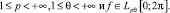
Если для некоторого q: 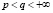 ряд
ряд
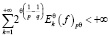
сходится, то 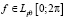 и справедливы неравенства:
и справедливы неравенства:
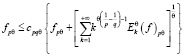 ,
,
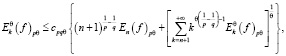
где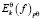 – наилучшее приближение функций f∈Lpθ[0; 2π].
– наилучшее приближение функций f∈Lpθ[0; 2π].
Доказательство. Пусть f∈Lpθ[0; 2π]. Tn(x) тригонометрический многочлен наилучшего приближения функций f
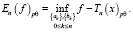
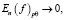 при
при 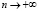 ,
, 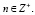
Пусть 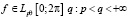 .
.
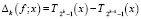 ,
,
где Tn(x) – многочлен наилучшего приближения функций f∈Lpθ[0; 2π].
Тогда согласно теореме 1 при m < n имеем
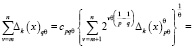
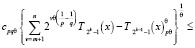
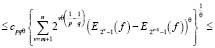
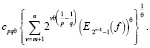 (1)
(1)
Так как ряды
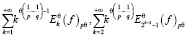
сходятся или расходятся вместе, то в силу условия теоремы правая сторона последнего неравенства стремится к нулю при (m, n) > +∞.
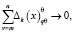 при min(m, n) > +∞.
при min(m, n) > +∞.
Следовательно, последовательность 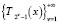 фундаментальна в метрике пространства Lpθ[0; 2π]. Так как пространство Lpθ[0; 2π] полно, то существует φ∈Lqθ[0; 2π] такая, что
фундаментальна в метрике пространства Lpθ[0; 2π]. Так как пространство Lpθ[0; 2π] полно, то существует φ∈Lqθ[0; 2π] такая, что
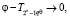 при v > +∞.
при v > +∞.
Следовательно, φ(x) симметрично к f(x) на [0; 2π]. Таким образом, f∈Lqθ[0; 2π].
Если же в (1) положим m = 2, n > +∞, тогда
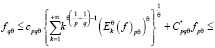
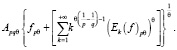
Теперь докажем второе неравенство.
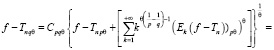
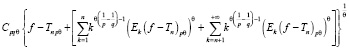 , (2)
, (2)
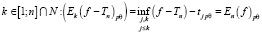 . (3)
. (3)
Теперь рассмотрим, когда ∀k > n:
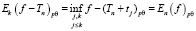 . (4)
. (4)
(3), (4) подставляем в (2):
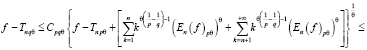
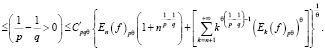
Таким образом, мы получили неравенство
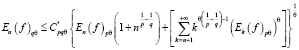 ,
, 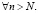
Теорема 3. Пусть 1 ≤ p < q < +∞, 1 ≤ θ < +∞ и f∈Lpθ[0; 2π]. Если для некоторого r∈N и 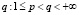 ряд
ряд
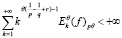
сходится, то существует производная 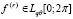 и имеют место неравенства
и имеют место неравенства
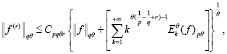
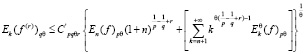

Здесь константы 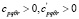 не зависят от f и
не зависят от f и 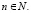
Доказательство. По условию теоремы ряд
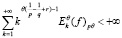
сходится. Поэтому
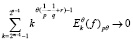
при 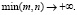 Тогда, согласно лемме 3, последовательность
Тогда, согласно лемме 3, последовательность 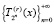 фундаментальна в пространстве Lpθ[0; 2π]. Поэтому, в силу полноты пространства Lpθ[0; 2π], существует
фундаментальна в пространстве Lpθ[0; 2π]. Поэтому, в силу полноты пространства Lpθ[0; 2π], существует
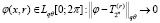
при n > +∞ Так как из условий теоремы также следует, что 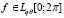 и
и
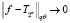 при n > +∞,
при n > +∞,
то 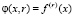 – в смысле С.М. Никольского. В лемме 3 положим m = 1 и n > +∞ Тогда
– в смысле С.М. Никольского. В лемме 3 положим m = 1 и n > +∞ Тогда
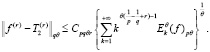
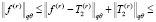
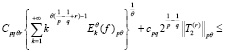
≤ (лемма 1) 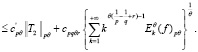
Так как
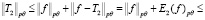
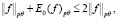
то
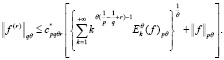
Теперь докажем второе неравенство:
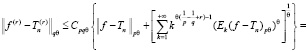
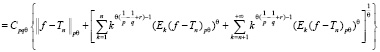 . (1)
. (1)
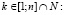
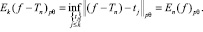 (2)
(2)
Пусть k > n:
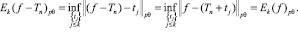 (3)
(3)
Далее (2), (3) подставляем в (1):
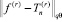
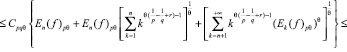
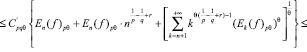
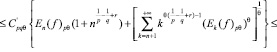
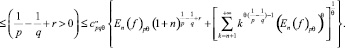
Таким образом, мы получили неравенство
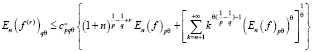
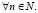
Теорема доказана.
Библиографическая ссылка
Муратова Г.К., Нурпейсова А.А. НЕРАВЕНСТВА В РАЗНЫХ МЕТРИКАХ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ НАИЛУЧШИМИ ПРИБЛИЖЕНИЯМИ В ПРОСТРАНСТВЕ ЛОРЕНЦА // Международный журнал прикладных и фундаментальных исследований. 2018. № 7. С. 61-66;URL: https://applied-research.ru/ru/article/view?id=12330 (дата обращения: 11.02.2026).

