Эта классическая задача оптимального управления ранее была неоднократно решена и результаты представлены в таких работах, как [1, 2]. Следует, однако, отметить, что для аэродинамического сопротивления в них были использованы упрощенные зависимости. В [1] полуэмпирическая формула для аэродинамического сопротивления
Xаэр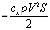 ,
,
где сx – коэффициент аэродинамического сопротивления, ρ – плотность воздуха, зависящая от высоты, V – скорость полета, S – характерная площадь летательного аппарата (в данной задаче площадь миделя ракеты) применялась с допущениями: сx = const, плотность воздуха аппроксимировалась экспоненциальной зависимостью по высоте 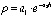 . Положительные коэффициенты a1, a2, вероятно, были подобраны методом наименьших квадратов. Из экспериментальных данных известно, что коэффициент аэродинамического сопротивления сильно зависит от числа Маха полета (рис. 1 из [3]), а кривая плотности, рассчитанная в соответствии с [4], не очень точно аппроксимируется экспоненциальной зависимостью (рис. 2).
. Положительные коэффициенты a1, a2, вероятно, были подобраны методом наименьших квадратов. Из экспериментальных данных известно, что коэффициент аэродинамического сопротивления сильно зависит от числа Маха полета (рис. 1 из [3]), а кривая плотности, рассчитанная в соответствии с [4], не очень точно аппроксимируется экспоненциальной зависимостью (рис. 2).
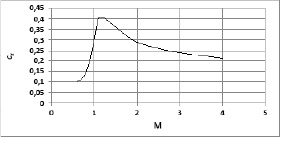
Рис. 1. Коэффициент аэродинамического сопротивления ракеты при угле атаки равном нулю в зависимости от числа Маха
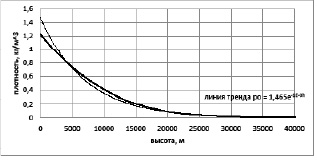
Рис. 2. Аппроксимация плотности воздуха по высоте экспоненциальной зависимостью
В работе [2] также принималось постоянство коэффициента аэродинамического сопротивления.
Качественное решение задачи ОУ выглядит следующим образом: в начале взлета двигатель должен работать на максимальном режиме, далее следует участок особого режима управления с пониженной тягой, по окончанию топлива – движение по инерции до некоторой высоты.
Цель исследования: провести численный эксперимент для метеорологической ракеты типа МР20 с уточнением математической модели для аэродинамического сопротивления в соответствии с [3] и [4], по полученным количественным результатам расчетов провести анализ целесообразности применения особого режима управления.
Математические модели и численные методы
При заданном весовом балансе ракеты будем максимизировать высоту подъема ракеты.
J = hподъема → max или
интегральный критерий 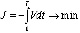
Система уравнений движения при вертикальном подъеме ракеты-зонда:
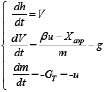
где h – высота, м; V – скорость, м/с; Р = βu тяга двигателя, Н; β – импульс РДТТ, м/с; u = GT – управление, расход топлива, кг/с; Xаэр – сила аэродинамического сопротивления, Н; m – масса ракеты, кг; t – время, с; 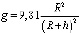 – ускорение свободного падения, м/с2, R – радиус Земли. В качестве исходных данных были приняты технические характеристики метеорологической ракеты МР-20: калибр dmax = 450 мм, взлетная масса m0 = 1620 кг, импульс двигателя β = 2011 м/сек считался постоянным, максимальный расход топлива u = GТ = 50,54 кг/сек, масса топлива 1200 кг.
– ускорение свободного падения, м/с2, R – радиус Земли. В качестве исходных данных были приняты технические характеристики метеорологической ракеты МР-20: калибр dmax = 450 мм, взлетная масса m0 = 1620 кг, импульс двигателя β = 2011 м/сек считался постоянным, максимальный расход топлива u = GТ = 50,54 кг/сек, масса топлива 1200 кг.
При использовании принципа максимума Понтрягина функция Понтрягина имеет вид
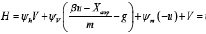
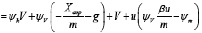 .
.
ψh, ψV, ψm – сопряженные переменные.
Функция линейна по управлению, коэффициент при управлении – функция переключения
Фпер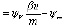 .
.
Оптимальное управление в этом случае
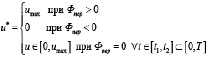
Последний случай относится как раз к особому режиму управления. Исследованиям управления с особым режимом посвящены такие работы, как [5, 6, 7]. В этом случае должно выполняться на [t1, t2]
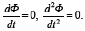
Вначале был рассмотрен случай без особого режима управления, решение краевой задачи для системы ДУ
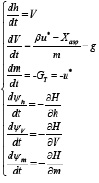
с краевыми условиями:
h(0) = 0, V(0) = 0, m(0) = m0 = 1620 кг,
V(Т) = 0, m(Т) = m0 – mтопл = 420 кг, ψh(Т) = 0
было получено методом пристрелки. Метод пристрелки или стрельбы дает наиболее точные результаты численного решения краевых задач [1, 8]. Производные функции Понтрягина по сопряженным переменным вычислялись с учетом того, что плотность воздуха, скорость звука и, соответственно, число Маха полета, а следовательно, и коэффициент аэродинамического сопротивления являются функциями высоты. Коэффициент аэродинамического сопротивления является также еще и функцией скорости полета. Внешний цикл – модифицированный метод Ньютона обращался к численному методу решения задачи Коши – методу Рунге – Кутты 4-го порядка. Для сходимости метода Ньютона момент отключения двигателя по израсходованию запаса топлива уточнялся линейной интерполяцией массы ракеты на шаге метода Рунге – Кутты, на котором заканчивалось топливо. После чего этот шаг пересчитывался с тягой двигателя, равной среднеинтегральному значению по указанному промежутку времени. Алгоритм пересчета был предложен для задач оптимального управления с переключением в [1], также применяя этот алгоритм, удалось достичь сходимости метода Ньютона в задачах с переключением в [9] и [10].
Параметры пристрелки и невязки для этого варианта расчета выбирались следующие:
ψh (0), ψV (0), ψm (0), Т,
δ1 = V(Т) → 0, δ2 = ψh(Т) → 0,
δ3 = H(Т) → 0, δ4 = Фпер(tпер ) → 0.
Полученные результаты не соответствовали теории: функция Понтрягина не была равна нулю на всем протяжении, функция переключения меняла знак дважды, причем в точке переключения меняла знак с минуса на плюс, а не наоборот. Таким образом, вывод о неоптимальности управления без особого режима подтвердился. При этом при обнулении силы аэродинамического сопротивления в математической модели функция переключения и функция Понтрягина вели себя согласно теории: функция Понтрягина была равна нулю с точностью до 4-го знака, функция переключения меняла знак один раз с плюса на минус именно в момент отключения двигателя в связи с израсходованием всего топлива.
Попытка реализовать алгоритм метода пристрелки для варианта с особым режимом управления при получении оптимального управления на особом режиме из равенства 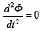 (полное выражение слишком громоздко и в силу этого не приводится) не увенчалась успехом. Оптимальное управление на особом режиме зависит от сопряженных переменных, которые являются параметрами пристрелки в начальный момент времени, и в процессе поиска решения методом Ньютона при неточно выбранном начальном приближении получаемые значения управления на особом режиме не удовлетворяют ограничениям: u ∈ [0, umax].
(полное выражение слишком громоздко и в силу этого не приводится) не увенчалась успехом. Оптимальное управление на особом режиме зависит от сопряженных переменных, которые являются параметрами пристрелки в начальный момент времени, и в процессе поиска решения методом Ньютона при неточно выбранном начальном приближении получаемые значения управления на особом режиме не удовлетворяют ограничениям: u ∈ [0, umax].
В силу указанных причин было принято решение отказаться от решения задачи методом пристрелки и реализовать более простой алгоритм с использованием результатов, полученных в предыдущих работах [1] (рис. 3), а именно, постоянства тяги на особом режиме управления.
Алгоритм расчета с двумя переключениями состоял в следующем: первый вызов метода Рунге–Кутты при максимальном значении тяги ограничивался временем t1, далее осуществлялся второй вызов метода Рунге–Кутты с пониженной тягой двигателя u = uotn ∙ umax, третий вызов при отключенном двигателе ограничивался достижением нулевой скорости полета. Были рассчитаны варианты при значениях t1 = 3, 5, 7, 9, 11 секунд. Для каждого из этих вариантов времени также варьировалась величина коэффициента уменьшения тяги uotn = 0,35; 0,45; 0,55; 0,65; 0,75, 0,85.
Таким образом, было получено решение для 30 вариантов управления тягой (+1 расчет без особого режима с временем работы двигателя около 24 с).
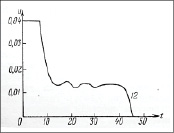
Рис. 3. 12-я итерация решения задачи о вертикальном подъеме ракеты-зонда методом проекции градиента [1]
Результаты расчетов
Результаты численного эксперимента для оптимального управления с участком особого режима представлены на рис. 4 и 5.
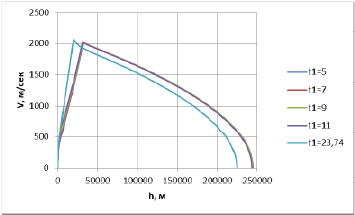
Рис. 4. Изменение скорости по высоте для uotn = 0,55 при разных значениях времени работы двигателя на максимальном режиме t1. Значение t1 = 23,74 с соответствует варианту без особого режима
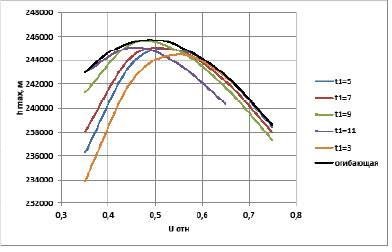
Рис. 5. Достижимая высота при различных вариантах регулирования двигателя
Заключение
Наличие особого режима управления связано с аэродинамическим сопротивлением воздуха, слишком быстрый набор скорости в плотных слоях атмосферы приводит к большим энергетическим потерям.
Численный метод пристрелки в промежуточных приближениях не дает возможности определения тяги на особом режиме в заданном диапазоне, что приводит к выводу о нецелесообразности применения этого метода для решения задач с переключением и наличием участка особого управления.
При работе на максимальном режиме около 8 с и дальнейшем уменьшении тяги двигателя до 50 % от максимального значения можно увеличить высоту подъема данной ракеты на 25 км, что составляет около 11 % от высоты, достигаемой без применения особого режима управления. Учитывая эти результаты, можно сделать вывод о незначительном увеличении эффективности с применением особого управления при решении подобных задач. С учетом необходимости создания твердотопливного реактивного двигателя с регулируемой тягой для реализации управления с особым режимом целесообразность применения особого режима становится спорной.
Библиографическая ссылка
Мозжорина Т.Ю., Попов А.С. РЕШЕНИЕ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ВЕРТИКАЛЬНЫМ ПОДЪЕМОМ РАКЕТЫ-ЗОНДА С УТОЧНЕНИЕМ МОДЕЛИ АЭРОДИНАМИЧЕСКОГО СОПРОТИВЛЕНИЯ // Международный журнал прикладных и фундаментальных исследований. 2021. № 7. С. 46-50;URL: https://applied-research.ru/ru/article/view?id=13247 (дата обращения: 11.02.2026).
DOI: https://doi.org/10.17513/mjpfi.13247

