Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Файлы

Ершина А.К. Каптагай Г.А.

Статья в формате PDF

883 KB

В статье изложены основы теории парусной ветротурбины. Теоретически определены аэро­динамические характеристики: коэффициенты подъемной силы и лобового сопротивления, мощность турбины, коэффициент использова­ния энергии ветра и др. Представлены сравне­ния результатов расчетов с экспериментальны­ми данными.

Наиболее прост расчет турбины парусного типа. В качестве примера рассмотрим работу четырехлопастный турбины, конструкция которой эскизно приведена на рис. 1 а. Каждая лопасть воспринимает давление ветра в полной мере при повороте с положения ОА в положение ОВ (см. рис. 1 б). За положением ОВ угол ата­ки становится отрицательным и кроме того по­является следующая лопасть, которая начинает затенять предыдущую. Таким образом, враща­тельный момент передается каждой лопасти в первый четверти описываемой ею окружности. Соответственно в этом квадранте сообщается передаваемая ветротурбине ветром мощность. Она расходуется на работу подъемной силы R и преодоление силы сопротивления лопасти.

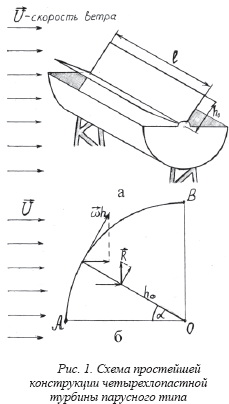
Свяжем систему координат с проворачивающейся в направлении движения ветра прямоугольной лопастью, площадь которой S₀=lh₀ м²

Тогда скорость набегания потока на лопасть будет равна где - ли­нейная скорость движения элемента лопасти на расстоянии h от оси вращения, - скорость ве­тра. Чтобы найти результирующую силу дина­мического давления, необходимо найти равнодействующую вектора относительной скорости воздушного потока. С этой целью проинтегри­руем последнее выражение по поверхности S₀=lh₀.

где

Динамическое давление ветра на лопасть 

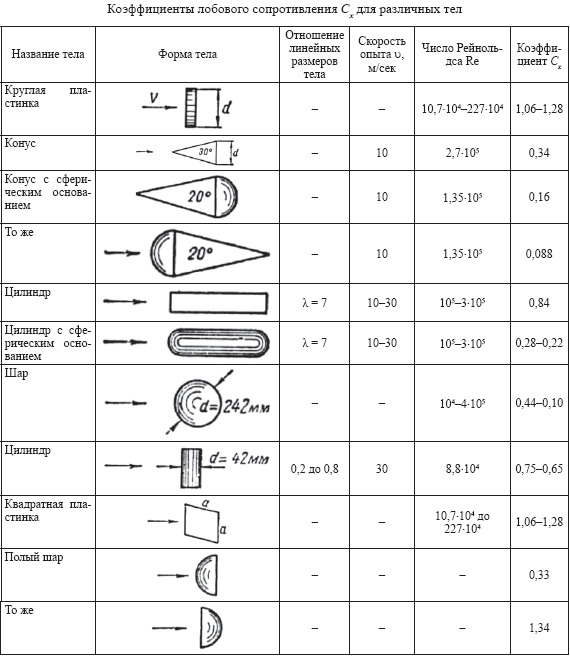
Сопротивление лопасти определим по известной формуле [1]

где(а) - коэффициент сопротивления прямоугольной пластины, пропорционален sin²(a) при малых углах атаки 0° ≤ a ≤ 20° [2] и C_x = 1,3 при a = 90° (см. таблицу), δ₁ - размеры вихревой до­рожки за пластиной, ширина которой δ₁ > h₀ при

В. Гейзенберг, приравняв циркуляцию, создаваемую в единицу времени на краях плоской пластины, расположенной нормально к потоку, циркуляции, переносимой вихрями, нашел, что    В нашем случае, когда срыв вихрей происходит лишь с одной стороны плоской лопасти, примем, что

Коэффициент сопротивления тонкого сим­метричного крылового профиля NASA 0006 в интервале изменения угла атаки 0° ≤ a ≤ 20° хо­рошо описывается эмпирической формулой:

Данных для углов атаки «a» больше 20° нет. При a ≤ 20° можно проинтерполировать и запи­сать зависимость, соответствующую большим углам атаки С_х = 1,3 при a→π/2

Таким образом формула (2) приобретает следующий вид

при 0° ≤α≤ 20°

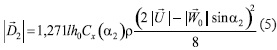
при α = α₂, 20° ≤ a₁ ≤ 90°.

Вектор подъемной силы направлен к скорости атаки под углом 90° и сила, действующая на подъем лопасти, равна

Принимая во внимание, что для пластины коэффициент подъемной силы С_у = 2πsina в интервале 0° ≤ a ≤ 20° [2] и R=0 при a₁ > 20°, можно определить мощность, передаваемую турбине ветром. Для этого следует подсчитать работу, совершаемую при перемещении лопасти из положения ОА в положение ОВ (см. рис. 1 б). При этом точка А пройдет путь равный      со скоростью Оютветственно, мощность, пере­даваемая турбине, будет равна

N = N_{l +} N₂,                                (7)

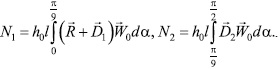
Принимая во внимание, что для пластины при 0° ≤ a ≤ 20°, C_y (a)= 2π sinα [3], и, подставляя выражения для с учетом (3) и (4), получим

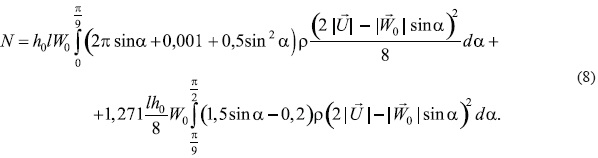
Интегралы - табличные, легко берутся. Проделав несложные операции, найдем: 

Коэффициент использования энергии ветра найдем, поделив переданную ветром турбине мощность N на собственную мощность ветра

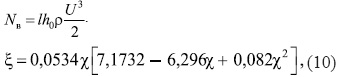
где - степень быстроходности ветротурбины. Приравняв первую производную нулю, найдем максимальную величину коэффициента использования энергии ветра ξ_max , а также значения χ, при которых достигаются ξ_max и ξ = 0. Итак ξ = 0 при χ = 0 и χ = 1,1568, а ξ_max = 0,1099 при χ = 0,576.

Мощность ветротурбины определяется фор­мулой

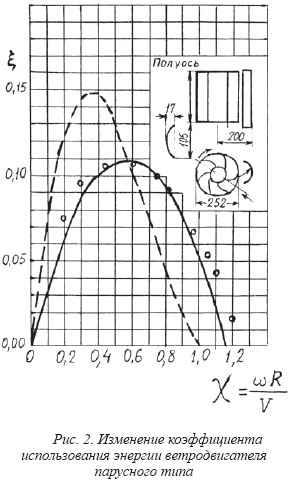
На рис. 2 представлены экспериментальные данные П.П. Осипова [3] и расчетные кривые по формуле (10), а также результаты расчета в предположении, что лопасть не вращается, а пе­ремещается поступательно со скоростью в направлении движения ветра [4]. Как видно из рис. 2, согласие расчётной кривой (10) с экспериментом отличается не более 10-15 %, тогда как максимальное отклонение пунктирной кри­вой значительно больше.

Список литературы

1. Чжен П. Отрывные течения. - М.: Мир, 1972.- Т.1, -299 с.

2. Лойцянский Л.Г. Механика жидкости и газа. - М.:Наука, 1987. -904 с.

3. Полторацкий В. Т. О работе ветродвигателя с осью вращения, расположенной перпендикулярно потоку // Отчет ЭНИИН АН СССР. - 1953.

4. Фатеев Е.М. Ветродвигатели и ветроустановки. - М.,1957. -536 с.

Библиографическая ссылка