В работе изучается сходимость разностных схем линейной модели океана. Исследуется сходимость итерационного метода по физическим факторам для линейных сеточных уравнений модели океана.
Рассмотрим краевые задачи модели океана в области Ω:
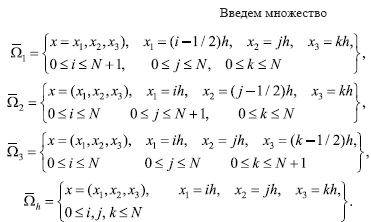
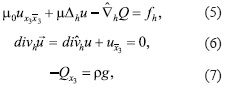
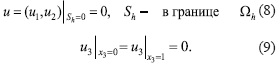
Теорема 1. Пусть решение задачи (1)-(4)
достаточно гладкое. Тогда имеет место оценка 
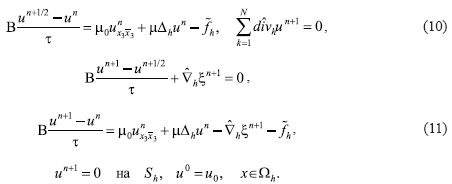
Отсюда
с условиями (11).
Введем пространство
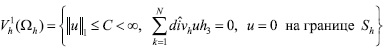
и пусть B - положительный ограниченный оператор, определенный на V1h (Ω). Схему (11), (12) можно записать в операторной форме
Оператор A - проекция оператора 
в пространство 
Предложим, что
Из общей теории итерационных методов легко доказывается [1]:
Теорема 2. Пусть выполнены условия (14). Тогда схема простой итерации (13) сходится к решению задач (3)-(4)
Список литературы
1.Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. - М.: Наука, 1978. - 590 с.
2.Кобельков Г.М. О численных методах решения уравнений Навье-Стокса в переменных скорости-давления // Вычислительные процессы и системы. - Вып. 8. - М.: Наука, 1991. -С. 204-230.
Библиографическая ссылка
Куттыкожаева Ш.Н., Наурызбаева А.А. СХОДИМОСТЬ РАЗНОСТНЫХ СХЕМ ДЛЯ ЛИНЕЙНЫХ МОДЕЛИ ОКЕАНА // Международный журнал прикладных и фундаментальных исследований. 2011. № 6. С. 83-84;URL: https://applied-research.ru/ru/article/view?id=1363 (дата обращения: 02.04.2025).