Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Файлы

Юров В.М. 1 Лауринас В.Ч. 1 Гученко С.А. 1 Завацкая О.Н. 1

---

1 Санкт-Петербург

Статья в формате PDF

456 KB

Для функции отклика системы частиц на разрушающее поле нами получено:

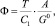(1)

где А – работа (энергия) разрушения; Т – температура; G0 – потенциал Гиббса; С1 – постоянная. По гипотезе Бонда полная работа разрушения пропорциональна среднему геометрическому между объемом и площадью вновь образуемой поверхности образца:

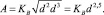(2)

Для малых частиц основную роль играет поверхность, так что G0 = σ⋅S = σ×pd2, σ – поверхностное натяжение. В качестве функции отклика системы на приложенное разрушающее напряжение возьмем функцию 1/(σТ – σМ). Тогда уравнение (1) примет вид:

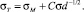(3)

Уравнение (3) по форме совпадает с уравнением Холла-Петча. Однако коэффициенты пропорциональности в обоих формулах различаются. В нашем случае поведение предела текучести малых частиц определяется также величиной их поверхностного натяжения σ. Для малых d А.И. Русанов получил асимптотическую линейную зависимость:

σ = Kd. (4)

Здесь К – коэффициент пропорциональности. Формула (4) получена на основе термодинамического рассмотрения и должна быть применима к малым объектам различной природы. В этом случае, уравнение (3) принимает вид:

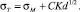(5)

Уравнение (5) показывает обратный эффект по отношению к уравнению Холла-Петча. Экспериментально этот эффект обнаружен для многих металлических частиц с размером менее 10 нм.

Библиографическая ссылка