Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Лаптев А.Г. 1 Лаптева Е.А. 1

---

1 ФГБОУ ВПО «Казанский государственный энергетический университет»

Рассмотрено применение модели локальной изотропной турбулентности для определения коэффициентов турбулентной вязкости в газожидкостном слое при пузырьковом и пенном режимах. Получены выражения для расчета коэффициентов турбулентной вязкости, связанные с динамической скоростью трения и средней скоростью диссипации энергии. Представлены результаты расчета данных коэффициентов при различных скоростях газа в барботажном слое.

Статья в формате PDF

1026 KB

изотропная турбулентность

газожидкостный слой

турбулентная вязкость

динамическая скорость

диссипация энергии

1. Кутателадзе С.С. Консервативные свойства пристенной турбулентности / С.С. Кутателадзе // ТОХТ. – 1971. – Т. 5, № 1. – С. 3–12.

2. Таунсенд А.А. Структура турбулентного потока с поперечным сдвигом. – М.: Наука, 1959. – 400 с.

3. Барабаш В.М. Процессы переноса в турбулентных потоках с интенсивным внешним источником турбулизации / В.М. Барабаш // Теор. основы хим. технол. – 1994. – Т. 28, № 2. – С. 110–117.

4. Kawase Y. Mathematical models for design of biorectors applications of Kolmogoroff’s theory of isotropic turbulence / Y. Kawase, M. Moo-Young // Chem. Eng. J. – 1990. – V. 43, № 5. – P. 1319–1341.

5. Лаптев А.Г. Математическое моделирование теплоотдачи при турбулентном обтекании пучков труб / А.Г. Лаптев, С.Г. Дьяконов, В.И. Елизаров // Теплоэнергетика. – 1992. – № 12. – С. 34–38.

6. Брагинский Л.Н. Перемешивание в жидких средах: физические основы и инженерные методы расчета / Л.Н. Брагинский, В.И. Бегачев, В.М. Барабаш. – Л.: Химия, 1984.

7. Доманский И.В. Обобщение различных случаев конвективного теплообмена с помощью полуэмпирической теории турбулентного переноса / И.В. Доманский, В.Н. Соколов // Теор. основы хим. технол. – 1968. – Т. 2, № 5. – С. 761–767.

8. Соколов В.Н. Газожидкостные реакторы / В.Н.Соколов, И.В.Доманский. – Л.: Машиностроение, 1976.

9. Лаптева Е.А., Фарахов Т.М. Модель турбулентной вязкости в барботажных аппаратах // Вестник КГЭУ, 2012, № 4. С. 26-33

10. Лаптев А.Г. Модели пограничного слоя и расчет тепломассообменных процессов. Казань: Изд-во Казан. ун-та, 2007. – 500 с.

11. Нигматуллин Р.И. Динамика многофазных сред / Р.И. Нигматуллин. – М.: Наука, 1987.

12. Шлихтинг Г. Теория пограничного слоя. / Г. Шлихтинг. – М.: Наука, 1974.

13. Броунштейн Б.И. Гидродинамика, массо- и теплообмен в колонных аппаратах / Б.И. Броунштейн, В.В. Щеголев. – Л.: Химия, 1988.

В промышленных аппаратах химической технологии и энергетических установках движение газов (паров) и жидкостей практически всегда происходит при турбулентном режиме. Поэтому для поиска путей совершенствования технологического и энергетического оборудования важное значение имеет достоверный расчет турбулентных течений.

Первые фундаментальные исследования турбулентных течений были выполнены еще в 19 веке Г. Гагеном, О. Рейнольдсом, Ж. Буссинеском, Г. Лоренцем и в начале 20 века развиты многими учеными (Л. Прандтль, Т. Кармен, В. Экман, И. Бюргерс, А. Колмогоров, Х. Драйден, Г. Клаузер, Дж. Тейлор, Г. Шлихтинг, Л. Лойцянский и др). Разработаны различные полуэмпирические теории пристенной турбулентности и отрывных течений. Осреднение по Рейнольдсу уравнений динамики вязкой жидкости приводит к системе уравнений Рейнольдса, называемые уравнениями для первых моментов. В общем случае проблема замыкания этих уравнений сводится к установлению связи тензора турбулентных напряжений с тензором осредненных скоростей деформаций.

Одна из первых попыток упростить расчет турбулентных течений принадлежит Буссинеску, который ввел понятие турбулентной вязкости. Далее эта гипотеза была развита Прандтлем и Карманом. При этом делались различные допущения о характере изменения коэффициента 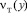. Опытами было установлено, что nт изменяется по поперечному сечению потока, возрастая по мере удаления от стенки до некоторого максимума и затем убывая на оси потока. Часто с достаточной для практических расчетов принимают среднее значение 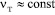в ядре потока, т.е. за пределами пристенного слоя.

Целью данной работы является получить приближенные расчетные выражения для коэффициента средней турбулентной вязкости в барботажном слое.

Коэффициент турбулентной вязкости

Рассмотрим теоретический подход определения коэффициента турбулентной вязкости в ядре потока, связанный со скоростью диссипации энергии турбулентности.

Коэффициент турбулентной вязкости по определению записывается в виде:

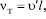(1)

где u′ – пульсационная скорость, м/с; l – масштаб турбулентного движения, м.

В вязком подслое 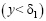[1]

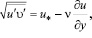(2)

где u′, u′ – продольная и поперечная составляющая пульсационной скорости, м/с; u* – динамическая скорость трения, м/с; u – продольная скорость в пограничном слое, м/с; y –поперечная координата, м; δ1 – толщина вязкого подслоя, м; n – коэффициент кинематической вязкости, м2/с.

а в основной зоне генерации турбулентности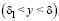

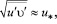(3)

где d – толщина гидродинамического пограничного слоя, м.

Во внешней части пограничного слоя (окрестности оси канала)

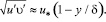(4)

Для основной зоны генерации турбулентности коэффициент турбулентной вязкости (1) с учетом (3) получит вид

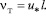(5)

Принимая модель локальной изотропной турбулентности запишем скорость диссипации энергии [2]

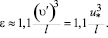(6)

Из выражений (5) и (6) получим среднее значение nт при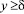

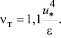(7)

Как отмечено, выражение (6) имеет более широкую область применения [3-9], а не только для условий локальной однородности и изотропности потока.

Турбулентность в жидкой фазе

При исследовании гидродинамики барботажного слоя обычно определяют коэффициенты продольного и поперечного перемешивания, которые связаны с режимом работы аппарата и его конструкцией. Как правило, коэффициенты перемешивания всегда больше коэффициента турбулентной вязкости. Только при малых скоростях газа основную роль в продольном перемешивании играют турбулентные пульсации, обусловленные деформациями газовых пузырей и заполнением жидкостью покинутого им объема, то есть турбулентностью в следах за газовыми пузырями.

Рассмотрим два режима барботажа в газожидкостных аппаратах [8]:

Пузырьковый режим с малым газосодержанием 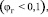когда расстояние между пузырьками больше их диаметра и стесненностью можно пренебречь.

При скорости газа на полное сечение барботажного аппарата (без учета жидкости) 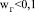м/с выражение для расчета динамической скорости получено в виде 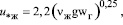[8].

(8)

а при 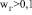м/с

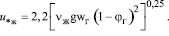(9)

где ϕг – среднее объемное газосодержание.

Газосодержание вычисляется по известным эмпирическим выражениям [8], например по формуле

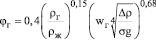, (10)

где ρг, ρж – плотности газа и жидкости, кг/м3; s –поверхностное натяжение, Н/м; ∆ρ – разность плотностей жидкости и пузырька, кг/м3.

При выводе выражений (8), (9) было принято, что газ барботирует в условно неподвижную жидкость.

В выражении (7) составляющую от средней скорости диссипации энергии в окрестности пузырька (в пограничном слое и вихревом следе) запишем в виде

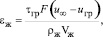(11)

τгр – среднее касательное напряжение на поверхности пузырей, Па; 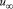– скорость движения пузырей, м/с; uгр – скорость движения межфазной поверхности, м/с; Vж – объем жидкости, где происходит диссипация энергии, м3; F – площадь поверхности пузырька, м2.

Учитывая, что толщина гидродинамического слоя на пузырьке на порядок меньше его диаметра запишем объем в виде суммы

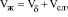(12)

где Vсл – объем вихревого следа за пузырьком, м3; 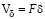– объем пограничного слоя на пузырьке, м3; d – средняя толщина пограничного слоя, м.

Представляя объем вихревого следа в виде полуэллипсоида вращения, в центр которого вписана дисперсная частица (пузырек), запишем [10]

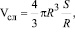(13)

где R – радиус пузырька, м; S – длина вихревого следа, м.

При числах 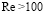длина вихревого следа примерно равна [11]

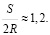(14)

Тогда 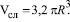(15)

Тогда из (11) – (15) при F = 4πR2 получим

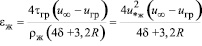(16)

и выражение (7) запишется в виде

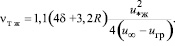(17)

Учитывая, что 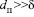среднюю толщину пограничного слоя найдем из выражения для пластины с учетом движения межфазной поверхности [12]

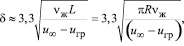(18)

где L = πR полупериметр длины обтекания пузырька, м.

Известно также выражение 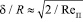[13]; 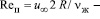число Рейнольдса для пузырька.

Среднюю скорость на границе раздела можно вычислить, используя функцию Адамара – Рыбчинского

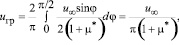(19)

где 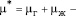отношение коэффициентов динамической вязкости дисперсной и сплошной фаз; j –угол.

В выражениях (17), (18) диаметр dп =2R и скорость всплытия пузыря вычисляются по известным зависимостям

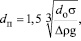(20)

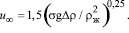(21)

где do – диаметр отверстия барботера, м.

Из (7), (8) и (17) в итоге получим

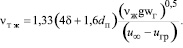(22)

Режим стесненного движения пузырей.

Переход к такому режиму можно оценить по условию 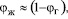где jж – удельный объем жидкости, находящийся в пограничных слоях всех пузырей и их вихревых следах. Из геометрических выводов имеем 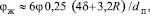Как показывают расчеты, для системы воздух – вода, такой режим начинается при 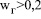м/с.

Если 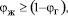то имеем 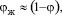и при таком режиме энергия диссипирует во всем объеме жидкой фазы и в газовых пузырях. Тогда выражение (11) запишем, используя удельную поверхность газожидкостного слоя

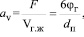(23)

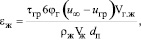(24)

где Vг.ж – объем газожидкостного слоя, м3; Vж – объем жидкости в слое, м3.

Если скорость газа в слое превышает скорость свободного всплытия пузыря, то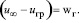

Учитывая связь

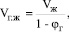(25)

уравнение (24) получит форму

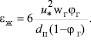(26)

Из (7) и (26) получим

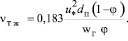(27)

где диаметр пузырьков

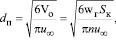(28)

где Vo – расход газа через отверстие, м3/с; Sк – площадь поперечного сечения аппарата, м2; n – число отверстий в барботере.

Окончательно с u* (9) имеем

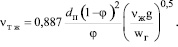(29)

На рисунке дана зависимость nтж от скорости газа в барботажном слое.

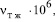м2/с

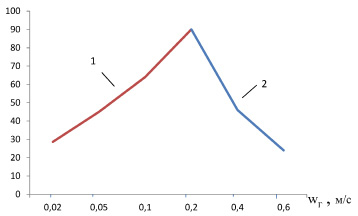
Зависимость коэффициента nтж от скорости газа: 1 – расчет по (22); 2 – расчет по (29). Система воздух – вода

Выводы

В статье на основе использования модели локальной изотропной турбулентности получены выражения для приближенного расчета средних значений коэффициента турбулентной вязкости в ядре жидкой фазы барботажного слоя. В результате расчетов получено, что при небольших скоростях газа 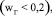и как следствие малых значениях газосодержания 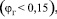коэффициент турбулентной вязкости увеличивается с повышением скорости газа, примерно 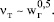Этот режим характеризуется нестесненным движением пузырей и турбулентность вызвана, главным образом вихревым следом. При 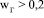м/с начинается стесненное движение пузырей и с повышением скорости газа коэффициент турбулентной вязкости значительно снижается. Это можно объяснить уменьшением масштаба турбулентности l в выражении (5), так как расстояние между пузырями уменьшается. При скоростях газа 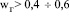м/с в отверстиях барботера образуются газовые струи (факелы), которые являются источниками генерации турбулентности. Для такого режима расчет ведется с учетом газовых струй [9].

Полученные выражения (22) и (29) пригодны для 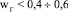м/с и могут использоваться для расчетов высокослойных барботажных реакторов, аэротенков, флотаторов и других аппаратов с газожидкостными средами, когда концевыми (входными) эффектами можно пренебречь.

Библиографическая ссылка