Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Жунусова Л.Х. 1 Тойганбаева Н.А. 1 Текесбаева Н.А. 1

---

1 Казахский национальный педагогический университет им. Абая

В настоящее время существует способ теоретического исследования сложных процессов, допускающих математическое описание, компьютерный эксперимент, т .е. исследование естественнонаучных проблем методами вычислительной математики. Математическому исследованию предшествует выбор приближения, т.е. решение вопроса о том, какие факторы надо учесть, а каким можно пренебречь. После этого проводится исследование проблемы методом вычислительного эксперимента. В данной работе исследована задача устойчивости и стабилизации системы описывающих биологический процесс. Получено стабилизирующее управление для исследуемой модели, который обеспечивает устойчивость решение на определенным отрезоке времени.

Статья в формате PDF

1057 KB

билинейная система

стабилизация

управление

аппроксимация

1. Бияров Т.Н. Устойчивость движения при постоянно действующих возмущениях. – Алматы: КазНУ, 1989. – 80 с.

2. Джолдасбеков О.А., Бияров Т.Н. Устойчивость и стабилизация движения механизмов и машин – Алматы: ИА РК, 1992. – 82 с.

3. Малкин Н.Г. Теория устойчивости движения. – М.: Наука, 1966. – 530 с.

5. Жунусова Л.Х. Об устойчивости и стабилизации билинейных моделей. //Функциональные пространства, теория приближений, нелинейный анализ, посвященной 100-летию академика С.М. Никольского: тезисы докладов международной конференции 5-7 мая 2005. – М. – 2005. – С.105.

6. Бияров Т.Н. Вопросы управляемости некоторых моделей // Проблемы современной математики и механики: тезисы докладов международной конференции 5-10 октбярь 2005./ Т.Н. Бияров, Л.Х. Жунусова – Алматы. – 2005. – С. 68.

7. Жунусова Л.Х. The solutions of a sum of control optimization in the class of bilinear systems // Вестник НАН РК № 5, 2007. – С. 26-28.

Известно, что структура различных иммунных процессов носит существенно нелинейный, распределенных и стохостический характер, ведущие процессы в большинстве случаев являются билинейными. Если судить по аналогии, то билинейные системы появляются при описании взаимодействие молекул антител с чужеродным веществом.

Анализ биологических систем и управление ими допустимо на основе билинейных моделей, если взаимодействия между составляющими можно будет описать с помощью временных линейнных уравнении, принимающих значения из некоторого множества и определяющих действие иерархии. В данной работе рассмотрена система на основе билинейных моделей. Биологическая система требует преодоления жестких ограничении, связанных с требованиями линейности. Другая ее особенность-эта изменчивая структура. Эта свойства является важным в тех случаях, когда на управления накладывается ограничения.

Лемма. Управления вида

осуществляет стабилизацию движения системы:

;

.

Доказательства данной леммы можно найти [1, 2, 3].

Постановка задачи. Выбором управления требуется стабилизировать движения на конечном отрезке времени.

Пусть тогда стабилизирующее управление можно предоставить в виде:

Для решения поставленной задачи взят процесс управления периодическим течением болезни [4, 5]. Этот процесс может быть описан:

,

,

с начальными условиями: ; :; :,

где первое уравнение описывает концентрацию зрелых плазмацитов, второе уравнение концентрацию антигена третье уравнение описывает концентрацию антител [6, 7].

Используем линеаризованную систему данной модели, которой получаем, пренебрегая членами x2x3.

Тогда матрица системы имеет вид:

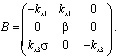
Теперь вычислим собственные значения матрицы:

Как видно решения неустойчивое и мы рассматриваемой модели добавляем стабилизирующее управления на конечном отрезке:

Фундаментальная матрица определяется из уравнения:

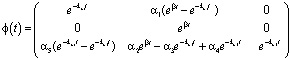
Теперь вычислим

Тогда имеем

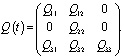
После вычислим элементы матрицы:

Далее находим

Таким образом, решение рассматриваемой системы при стабилизирующем управлении имеет вид:

А стабилизирующее управление имеет вид:

Эти найденные выражения определют программное управление. Кроме этого, мы задачу исследовали с помощью численных методов.

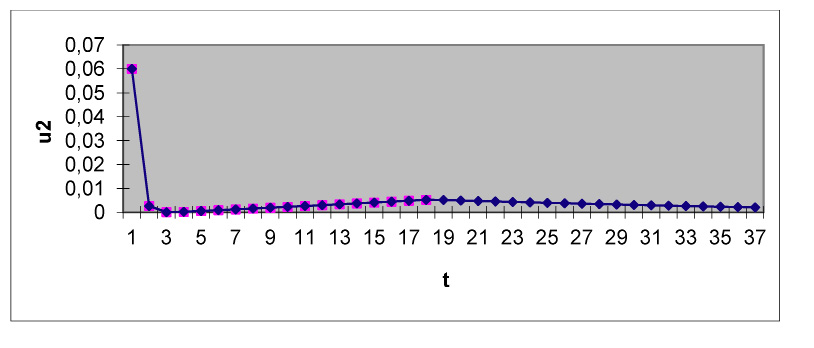
Изображение поведения управления u2 при 1,70<х1<1,89 , 5.1<х2<3.2, 0.9< х3<6.5

Рисунок показывает изменение поведения управления, в частности, u2. Именно u2 заменяет билинейность во втором уравнении системы моделируемого процесса. Как видно, в начальный момент времени значении u2 резко падает и даже достигает нулевого значения. Затем, через два часа, опять восстановливает свое значение и так плавно приближается к нулю.

Заключение. Оценку близости аппроксимационной модели можно получить, выбирая продолжительность времени . Таким образом, мы можем приближенно находить решение билинейной системы через решения линеаризованной системы, обеспечивающее стабилизацию системы на конечном отрезке времени.

Библиографическая ссылка