1018 KB
1. Левитан Б.М., Саргсян И.С. Введение в спектральную теорию. – М.: Наука, 1970. – 672 с.
2. Митрохин С.И. Спектральные свойства краевых задач для функционально-дифференциальных уравнений с суммируемыми коэффициентами // Дифференциальные уравнения. – 2010. – Т. 46. № 8. – С.1085-1093.
Изучим асимптотику решений дифференциального уравнения Штурма-Лиувилля:
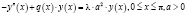, (1)
где λ – спектральный параметр, потенциал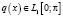 
– суммируемая функция.
Функциями Йоста (см. [1, глава 1]) называются решения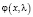 
и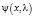 
уравнения (1), удовлетворяющие начальным условиям
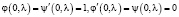. (2)
Методами главы 5 монографии [1] и работы [2] доказывается следующая теорема.
Теорема. Функции Йоста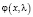 
(функция типа косинуса ) и 
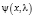(функция типа синуса), при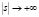 
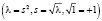имеют следующие асимптотические разложения:
,
,
,
,
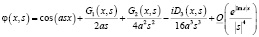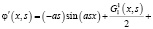
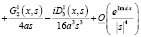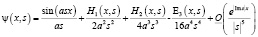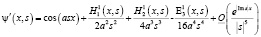при этом
,
.
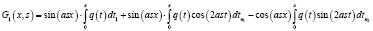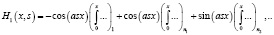Библиографическая ссылка
Митрохин С.И. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ ФУНКЦИЙ ЙОСТА В СЛУЧАЕ СУММИРУЕМОГО ПОТЕНЦИАЛА // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 1-2. – С. 282-283;URL: https://applied-research.ru/ru/article/view?id=4676 (дата обращения: 21.11.2024).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
«Международный журнал прикладных и фундаментальных исследований»
ИФ РИНЦ = 0,593
«Международный журнал экспериментального образования»
ИФ РИНЦ = 0,425
«Научное Обозрение. Биологические Науки»
ИФ РИНЦ = 0,400
«Научное Обозрение. Медицинские Науки»
ИФ РИНЦ = 0,801
«Научное Обозрение. Экономические Науки»
ИФ РИНЦ = 0,871
«Научное Обозрение. Педагогические Науки»
ИФ РИНЦ = 0,733
«Научное Обозрение. Технические Науки»
ИФ РИНЦ = 0,695
«European journal of natural history»
ИФ РИНЦ = 0,301