Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Догучаева С.М. 1

---

1 Финансовый университет при Правительстве Российской Федерации

Оптимизация управления и проектирования естественных факторов среды является практически важной областью применения методов математического моделирования природных процессов. В практике научных вычислений при приближенном решении нестационарных задач математической физики все большее внимание уделяется вычислительным алгоритмам повышенной точности [1]. Проблемы воздействия естественных и антропогенных факторов окружающей среды, должны трактоваться как единственно нелинейные, так как линейный подход не позволяет описывать реально наблюдаемые эффекты пространственной локализации (при линейном подходе скорость распространения загрязняющих веществ мгновенна) и стабилизации за конечное время. В то же время это значительно усложняет математические модели, приводя к необходимости исследования локальных и нелокальных задач со свободной границей для нелинейного параболического уравнения. Постоянно изменяющаяся экологическая ситуация требует специальных алгоритмов решения обратных задач, способных работать в реальном времени. Одна из основных задач нашего времени – это организация подготовки специалистов в области геоинформационных технологий и обработки данных с помощью новых аппаратно – программных средств.

Статья в формате PDF

1110 KB

Поверхности уровня поля концентрации

функция источников

функция стоков

диффузионные процессы

1. Вабищевич П. Н. Двухслойные схемы повышенного порядка аппроксимации для нестационарных задач математической физики // Ж. вычисл. матем. и матем. физ. – 2010. – Т.50. – №1. – С. 118–130.

2. Вабищевич П.Н. Самарский А.А. Монотонные разностные схемы для задач конвекции-диффузии на треугольных сетках // Ж. вычисл. матем. и матем. физ. – 2002. – Т. 42. № 9. – С. 1368. – 1382.

3. Догучаева С.М. Качественное исследование нелинейных задач параболического типа в области применения новых информационных технологий. «Информатизация и связь». -М:2013 №1.- С.31-34.

4. Догучаева С.М. Системный подход в экономико-математическом моделировании // Научные итоги 2013 года: достижения, проекты, гипотезы. – Новосбирск: 2013. – С. 167-172.

5. Догучаева С.М. Новые процессы разработки для определения эколого-экономической ценности природных ресурсов// Международный технико-экономический журнал. – М: 2013 №6. – С.74-78.

6. Марчук Г.И. Математическое моделирование в проблемах окружающей среды. – М.: Наука, 1982. – 320 с.

7. Шишкин Г.И., Аппроксимация систем сингулярно возмущенных эллиптических уравнений реакции-диффузии с двумя параметрами // Ж. вычисл. матем. и матем. физ. – М.: 2007. – Т. 47. № 5. – С 835 – 866.

Сложный многоуровневый характер природных процессов делает практически невозможным их точный математический расчет, в связи с этим, уже на стадии математического моделирования для создания численно аналитических методов расчета, реализуемых с помощью компьютерных технологий и программного обеспечения, приходится делить их на несколько подуровней. [5] Особенный интерес при изучении задач локального загрязнения окружающей среды представляют тяжелые аэрозоли. [4]. Диффузионные процессы, протекающие в атмосфере и океане, представляют собой практически важную задачу, связанную с решением различных проблем защиты окружающей среды от загрязнения [3]. Как правило, эти процессы носят турбулентный [3] характер и поэтому их теоретическое исследование сопряжено с большими трудностями, возникающими уже на стадии создания и выбором конкретных зависимостей коэффициента турбулентной диффузии K времени T, стоками f(c) и концентрацией диффундирующих примесей c. [4,5] Такое описание возможно только на основании нелинейных моделей, отражающих зависимость турбулентного коэффициента диффузии от концентрации, а также учета ее поглощения, к рассмотрению которых мы и переходим.

При прогнозировании, управлении и оптимизации процессов адвективного переноса и диффузии определяющим являются не поле концентрации c(p,t) [4], а поле поверхности ее уровня. Поэтому в тех случаях, когда это возможно, естественна и необходима формулировка задач со свободными границами [3] в терминах этих определяющих величин, несмотря на существенное усложнение дифференциального уравнения [5], начального и краевых условий [4].

В случаях стремления коэффициента диффузии к нулю в окрестности границы возникают пограничные слои [7]. Но это уже другие постановки задач диффузионных процессов.

В данной работе мы рассмотрим задачу Дирихле для поверхностей уровня поля концентраций. Источник загрязнения здесь обозначается через w. [3]

Постановка задачи. Если на известной части S(t) ограниченной поверхности области W(t) задано краевое условие Дирихле, то для определения поля концентраций c(P,t) и свободной поверхности 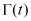: 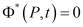получаем систему уравнений:

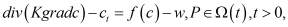
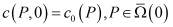
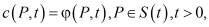(1)

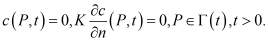
Поверхности уровня скалярного поля концентрации 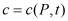[5] определяет в неявной форме однопараметрическое семейство поверхностей уровня 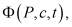где 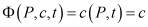. Если краевое условие Дирихле таково, что область W(t) расслаивается изотермическими поверхностями, то концентрацию с можно считать монотонной функцией одной из координат, например, z, при фиксированных значениях x,y,t. Это дает возможность с помощью специального преобразования типа Мизеса 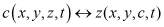перейти от задачи определения поля концентрации 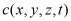к задаче определения поля ее поверхностей уровня 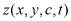. Такое преобразование позволяет избавиться от необходимости определения свободной поверхности [4], так как концентрация при этом выступает в роли независимой переменной и значение c=0 соответствует этой поверхности – 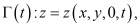и для поверхностей уровня 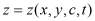получить следующую начально – краевую задачу:

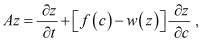
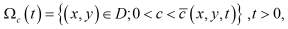
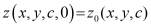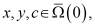, (2)

,

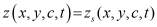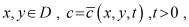
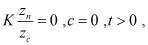
где 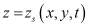– уравнение известной поверхности ;

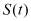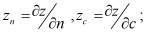
n – внешняя нормаль к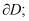

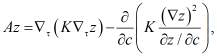(3)

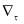– тангенциальная часть оператора 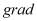. При постановке задачи (2) мы воспользовались формулами дифференцирования обратных функций, которые приводят к следующим соотношениям:

,

.

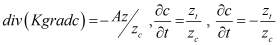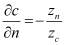Одномерная задача. В простейшем одномерном случае задача для определения поля концентраций 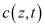и свободной поверхности Г(t) [3] и соответствующая задача относительно поля поверхности уровня z(c,t) записываются в виде

,

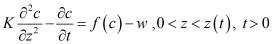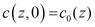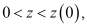, (1′)

, ,

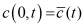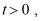
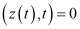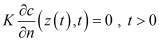, и

,

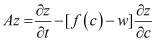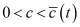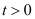, , (2')

, ,

,

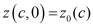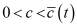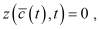
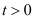где 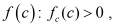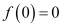– функция стоков; 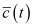– монотонно неубывающая функция времени

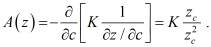(3′)

Монотонность оператора А и нахождение единственности решения задачи для поверхностей уровня (2′) в процессе загрязнения атмосферы.

Для установления свойства монотонности оператора A воспользуемся известной первой формулой Грина

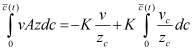. (4)

Полагая в (4) 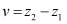и первый раз 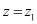, а второй 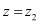, где 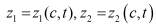– произвольные дважды непрерывно дифференцируемые функции, определенные на 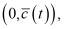получим два равенства

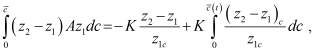(5)

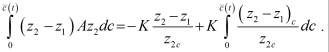(6)

Вычитая (5) из (6), получаем следующее соотношение:

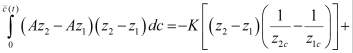
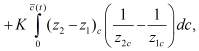
которое после простого преобразования подынтегрального выражения во втором слагаемом правой части записывается в виде

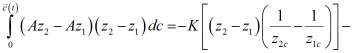
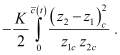(7)

Пусть теперь

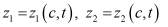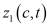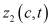– два различных решения задачи (2′). Тогда, в силу краевых условий первое слагаемое из (7) равно нулю, а подынтегральное выражение во втором слагаемом, в силу монотонности функций и по 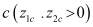, положительно. Следовательно, первая формула Грина для оператора задачи (2') окончательно запишется в виде

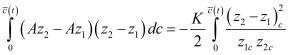. (8)

Так как правая часть равенства (8) не положительна, то отсюда следует монотонность оператора А на решениях задачи (2′).

Используя свойство монотонности оператора А, докажем единственность решения задачи (2′). Для этого с помощью дифференциального уравнения задачи исключим из (8) Az1 и Az1. Имеем

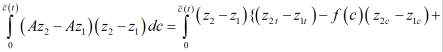
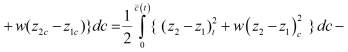
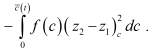(9)

Интегрируя по частям последний интеграл, учитывая граничные условия задачи (2′) свойства функции f(c), перепишем (9) в виде

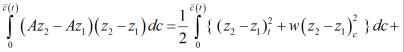
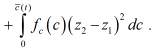(10)

Как нетрудно видеть, правая часть полученного равенства неотрицательна. Однако выше было сказано, что правая часть не положительна (см. (8)). Из полученного противоречия следует, что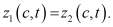

Таким образом, мы приходим к следующему основному выводу:

Если функция источников 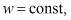функция стоков f(c) монотонно возрастает и 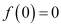, то решение одномерной задачи Дирихле (2′) для поверхностей уровня положительно и единственно.

К основным процессам самоочищения или рекреации, с учетом их результативности, следует отнести химические реакции, микробиологическое окисление, процессы адсорбции и распада. Восстановительная способность атмосферы представляется с помощью функции распределения стоков загрязнения f = f(c) [3].

При разработке неотложных мер по экологической проблеме, существенную роль играют математические модели переноса и диффузии в стратифицированных водной и воздушной средах, позволяющие производить расчеты и давать прогнозы. При построении разностных схем для задач гидродинамики, тепло- и массопереноса большое внимание уделяется так же монотонным схемам [2].

Современные практики и исследователи отмечают, что в настоящее время влияние человека на природу достигает такого размаха, что естественные регуляторные механизмы уже не в состоянии самостоятельно нейтрализовать многие нежелательные и вредные его последствия. Экологическая политика должна учитывать взаимозависимость между природными средами, технологиями производства, загрязнения и сокращения загрязнения, между самими загрязняющими веществами. Это, конечно необходимо учитывать при разработке долгосрочных программ [6].

Господствующие в обществе социальные установки оказывают решающее влияние на его экономику и системы управления. Надо уметь создавать перспективы, раскрывая потенциал сотрудников, клиентов и общества в целом [4]. Грань, отделяющая сегодняшнее состояние нашей планеты от экологической катастрофы настолько тонка, что речь надо вести не об «экологии вообще», а о размерах отклонений экологических характеристик нашей среды обитания от значений минимально необходимых для жизнедеятельности обитателей планеты.

Библиографическая ссылка