1
Лыжник Е.А. 1
1 Воронежский государственный университет инженерных технологий
1. Павловский В.А. К вопросу о теоретическом описании слабых водных растворов полимеров // Доклады АН СССР. – 1971. – Т. 200, № 4. – С. 809–812.
2. Осколков А.П. О нестационарных течениях вязко-упругих жидкостей // Труды МИАН СССР. – 1983. – Т. 159. – С. 103–131.
3. Осколков А.П. О единственности и разрешимости в целом краевых задач для уравнений движения водных растворов полимеров // Записки науч. семин. ЛОМИ. – 1973. – Т. 38. – С. 98–136.
4. Koрпусов М.О., Свешников А.Г. O разрушении решения системы уравнений Осколкова // Математический сборник. – 2009. – Т. 200. – № 4. – С. 83–108.
5. Барановский Е.С. Исследование математических моделей, описывающих течения жидкости Фойгта с линейной зависимостью компонент скорости от двух пространственных переменных // Вестник Воронежского государственного университета. Серия: Физика. Математика. – 2011. – № 1. – C. 77–93.
6. Барановский Е.С. Задача оптимального граничного управления для уравнений движения полимерных растворов // Математические труды. – 2013. – Т. 16, № 2. – C. 13–27.
7. Барановский Е.С. О течении полимерной жидкости в области с непроницаемыми границами // Журнал вычислительной математики и математической физики. – 2014. – Т. 54, № 10. – С. 91–98.
8. Kузнецова Ю.Л., Cкульский О.И., Пышнограй Г.В. Течение нелинейной упруговязкой жидкости в плоском канале под действием заданного градиента давления // Вычислительная механика сплошных сред. – 2010. – Т.3. – С. 55–69.
9. Барановский Е.С. О стационарном движении вязкоупругой жидкости типа Олдройда // Математический сборник. – 2014. – Т. 205, № 6. – C. 3–16.
10. Hron J., Roux C., Malek J., Rajagopal K.R. Flows of incompressible fluids subject to Navier’s slip on the boundary // Computers and Mathematics with Applications. – 2008. – Vol. 56. – P. 2128–2143.
11. Барановский Е.С. Задача оптимального управления стационарным течением среды Джеффриса при условии проскальзывания на границе // Сибирский журнал индустриальной математики. – 2014. – Т. 17, № 1. – C. 18–27.
В современных технологических процессах широко используются различные полимерные материалы. Предложено много моделей, описывающих движение полимерных сред. Удовлетворительное описание течения слабых водных растворов полимеров дает модель В.А. Павловского [1]. Уравнения этой модели активно исследовались А.П. Осколковым и другими авторами [2–7].
Рассмотрим задачу о торможении раствора полимеров в плоском канале. Пусть раствор заполняет полость между плоскостями z = 0, z = h. Предположим, что за счет перепада давления вдоль оси y жидкость приводится в движение, а потом внешняя сила перестает действовать. Требуется определить поле скоростей затухающего движения жидкости.
Используя методы решения задач Штурма-Лиувилля, получаем серию решений:
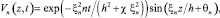 n = 1, 2, ….,
n = 1, 2, ….,
где Vn(z,t) –скорость жидкости вдоль оси y; n – вязкость раствора, ξn > 0 – корни уравнения
2ξnkh ctgξ – n2ξ2 + k2h2 = 0;
здесь k – коэффициент скольжения, k > 0, θn = arctg(nξn/kh). Применяя метод наложения, из набора Vn можно получить решение с заданным начальным условием.
В связи с полученными результатами стоит упомянуть работы [8–10], в которых изучаются различные модели, описывающие течения вязкоупругих жидкостей в плоском канале, и статью [11], в которой рассматривается задача управления течением вязкоупругой среды в условиях пристенного скольжения.
Библиографическая ссылка
Лыжник Е.А. ТОРМОЖЕНИЕ ТЕЧЕНИЯ ПОЛИМЕРНОЙ ЖИДКОСТИ В ПЛОСКОМ КАНАЛЕ // Международный журнал прикладных и фундаментальных исследований. 2014. № 9-3.
С. 168-168;
URL: https://applied-research.ru/ru/article/view?id=5903 (дата обращения: 07.03.2026).
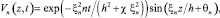 n = 1, 2, ….,
n = 1, 2, ….,

