Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Файлы
• Литература

Исаев Ю.М. 1 Семашкин Н.М. 1 Шигапов И.И. 1 Джабраилов Т.А. 1

---

1 ФГБОУ ВПО «Ульяновская государственная сельскохозяйственная академия имени П.А. Столыпина»

Статья в формате PDF

849 KB

1. Исаев Ю.М., Семашкин Н.М., Злобин В.А., Назарова Н.Н. Элементы теории спирально-винтового устройства с переменным шагом / Вестник Ульяновской государственной сельскохозяйственной академии. – 2013. – № 3 (23). – С. 117–121.

2. Исаев Ю.М., Воронина М.В., Семашкин Н.М., Злобин В.А. Влияние активного слоя на перемещение зерна в спирально-винтовом транспортере / Успехи современного естествознания. – 2008. – № 8. – С. 65–66.

Для нахождения рабочей площади поперечного сечения спирально-винтового устройства рассмотрим его уравнения двумерной поверхности:

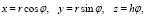
где 0<r<a, 0<φ<2π.

Элемент dS площади имеет вид:

.

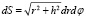Вычисляя интеграл получаем выражение для площади S:

.

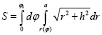Для определения уравнения 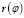нижнего предела интегрирования запишем уравнение прямой в отрезках:

,

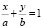где а – внешний радиус винтового устройства;

.

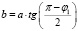Значение угла 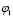находится по формуле: 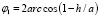. Обозначим 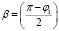и переходя к полярной системе координат 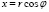, а 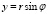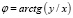, получим:

.

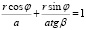Откуда окончательно получаем:

.

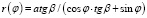Тогда интеграл для вычисления площади поверхности запишется:

.

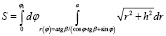При этих данных получается некоторое увеличение пропускной способности из-за конструктивных особенностей спирально-винтовых рабочих органов.

Библиографическая ссылка