Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Тимошенко Л.И. 1

---

1 Ставропольский филиал Краснодарского университета МВД России

Использование методов цифровой обработки сигналов позволяет относительно легко обеспечить высокую помехоустойчивость систем обработки данных, необходимую точность и разрешающую способность, стабильность параметров тракта обработки информации и ряд других преимуществ. При этом эффективность работы системы цифровой обработки сигналов во многом определяется математической моделью. Как правило задачи цифровой обработки сигналов требуют выполнения больших объемов вычислений над большими массивами данных в реальном масштабе времени. Возрастание требований к технико-экономическим характеристикам современных систем цифровой обработки сигналов, расширение их областей применения и усиливающаяся тенденция к параллельным методам их организации привели к активизации работ по разработке специализированных процессоров цифровой обработки сигналов, ориентированных на построение систем цифровой обработки сигналов с предельными значениями технических характеристик.

Статья в формате PDF

763 KB

цифровая обработка сигналов

арифметические операции

суммирование по модулю

нейронная сеть

системе остаточных классов

1. Адошев А.И., Аникуев С.В., Гальвас А.В., Жданов В.Г., Ивашина А.В., Кобозев В.А., Логачева Е.А., Привалов Е.Е., Тимошенко Л.И., Шарипов И.К. Современные технологии в образовании // Развитие системы образования – обеспечение будущего. – Одесса. – 2013. – С. 60-97.

2. Земцев А.М., Тимошенко Л.И. Информационная составляющая безопасной эксплуатации электроустановок // Методы и средства повышения эффективности технологических процессов в АПК: Опыт, проблемы и перспективы. – 2013. – С. 76-78.

3. Калмыков И.А., Тимошенко Л.И. Нейросетевые модели многовходовых сумматоров по модулю два // Фундаментальные исследования. – 2008. – № 3. – С. 73-74.

4. Калмыков И.А., Тимошенко Л.И. Систолическая матрица для цифровой фильтрации в модулярной арифметике // Современные наукоемкие технологии. – 2007. – № 11. – С. 98-100.

5. Калмыков И.А., Хайватов А.Б., Тимошенко Л.И., Гахов В.Р. Применение полиномиальной системы классов вычетов для повышения скорости функционирования спецпроцессора адаптивных средств защиты информации // Успехи современного естествознания. – 2007. – № 5. – С. 76.

6. Кузьменко И.П., Тимошенко Л.И. Систолические принципы организации вычислений в спецпроцессоре цифровой обработки сигналов с параллельно-конвейерным распределением вычислительного процесса // Культура и общество: история и современность: материалы II Всероссийской (с международным участием) научно-практической конференции. – Ставрополь. – 2013. – С. 76-78.

7. Тимошенко Л.И. Нейросетевая реализация вычислений в полиномиальной системе классов вычетов // Фундаментальные исследования. – 2008. – № 3. – С. 71-73.

8. Тимошенко Л.И. Информатика. Курс лекций: Учебное пособие / Филиал РГСУ в г. Ставрополе. Ставрополь. – 2014. – Том Часть 2.

9. Тимошенко Л.И. Анализ основных методов прямого преобразования из позиционной системы счисления в модулярный полиномиальный код // Современные наукоемкие технологии. – 2007. – № 9. – С. 23-24.

10. Тимошенко Л.И. Применение математической модели обладающей свойством кольца, для реализации цифровой обработки сигналов // Современные наукоемкие технологии. – 2007. – № 9. – С. 22-23.

Для эффективной реализации математических моделей цифровой обработки сигналов (ЦОС) определённых в кольце полиномов необходимо, чтобы вычислительные устройства могли эффективно поддерживать арифметические операции этой алгебраической системы. Рассмотрим выполнение таких операций в полиномиальной системе классов вычетов. Для этого необходимо представить значения остатков операндов в виде полиномиальной записи [5, 6]. Пусть степень неприводимого полинома . Тогда справедливо

. (1)

Аналогичным образом представим второй операнд

. (2)

Известно, что сравнения по одному и тому же модулю можно почленно складывать, то для суммы двух полиномов и , имеющих соответственно коды и  справедливо соотношения [9]

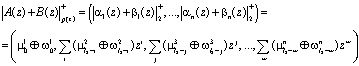(3)

где  – операция суммирования по модулю р.

Исходя из условия, что характеристика поля равна двум, то операция обратная суммированию выполняется аналогичным образом [8]:

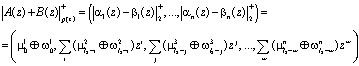(4)

В результате выполнения (3) и (4) получаются элементы образующие циклическую группу по операции сложения. Для реализации операции сложения -
разрядных операторов в поле по основанию потребуется всего двухвходовых сумматоров по модулю два. Причём базовая операция – сложение, реализуется за одну операцию и не требует применения итеративных методов построение нейронной сети (НС) конечного кольца, используемого в системе остаточных классов (СОК) [1,2].

Известно [10], что в силу дистрибутивности операции умножения операндов над кольцом на элементы этого кольца относительно операции сложения имеем

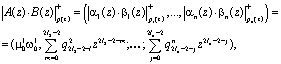(5)

где  – линейная свертка; ; .

Таким образом, выполнение операции умножения над операндами в кольце полиномов имеет вид

, (6)

Из выражений (5) и (6) наглядно видно, что реализация модульного умножения реализуется на основе умножения соответствующих остатков по основаниям с последующих суммированием по модулю характеристики поля. Следовательно, разработка высокоскоростного устройства, реализующего базовую операция по модулю характеристики поля в нейросетевом базисе, позволит обеспечить эффективную работу в реальном масштабе времени всего СП ЦОС[3,4].

Характерной чертой рассмотренных выше арифметических устройств, реализующих операции конечных алгебраических систем является наличие многовходовых сумматоров по модулю два [7]. Исходя из данной структурной особенности, можно сформулировать основные требования к нейронной сети, выполняющей эту базовую операцию:

– использование параллелизма, причем распараллеливание должно производится на уровне побитовой обработки входного вектора;

– применение конвейерной организации вычисления;

– отказ от принципа рекуррентной редукции, от обратных связях в структуре НС конечного кольца;

– количество итераций в процессе выполнения операции должно быть минимальным;

– количество нейронов в слоях НС должно быть минимальным, обеспечивая требуемую скорость обработки входного вектора.

Для повышения эффективности и достижения высоких показателей отказоустойчивости нейросетевых спецпроцессоров цифровой обработки сигналов является их построение на базе использования избыточности и корректирующих способностей алгебраической системы, которая положена в основу математической модели цифровой обработки сигнала. Применение полиномиальной системы классов вычетов позволяет не только повысить скорость обработки данных, но и обеспечить требуемый уровень надежности функционирования нейросетевого вычислительного устройства цифровой обработки сигналов.

Библиографическая ссылка