Рефракция растворов носит информации о структуре раствора и о растворении вещества в данном растворителе [1–4]. В этой работе числа гидратации ионов в разбавленных водных растворах некоторых электролитов были определены рефрактометрическим методом. Благодаря тому, что при оптических частотах диполи и ионы не успевают следить за изменениями направления электрического поля световой волны, основной вклад в поляризацию среды вносят электроны и в данном случае для водных растворов электролитов (KiAj) можно применить уравнение Лоренца-Лоренца [4]:
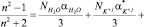
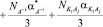 , (1)
, (1)
где, n показатель преломления рассматриваемого раствора, 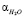 ,
, 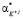 ,
, 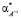 ,
, 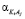 поляризуемости молекул воды, гидратированных катионов K+j валентности + j и анионов A–i валентности – i, нейтральных молекул KiAj (KiAj → iK+j + jA–i), соответственно,
поляризуемости молекул воды, гидратированных катионов K+j валентности + j и анионов A–i валентности – i, нейтральных молекул KiAj (KiAj → iK+j + jA–i), соответственно, 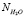 ,
, 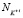 ,
, 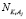 ,
, 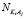 числа свободных молекул воды, катионов K+j и анионов A–i, нейтральных молекул KiAj в единичном объеме раствора, соответственно.
числа свободных молекул воды, катионов K+j и анионов A–i, нейтральных молекул KiAj в единичном объеме раствора, соответственно.
Члены в правой части уравнения (1) отражают вклады в общую поляризацию раствора, даваемые свободными, не вовлеченными в гидратацию молекулами воды, диссоциированными ионами K+j, A–i и недиссоциированными, нейтральными молекулами KiAj соответственно. Обозначая степень диссоциации KiAj через b, числа свободных молекул воды, ионов K+j, A–i и нейтральных молекул KiAj в единице объема раствора можно выразить через концентрацию KiAj в растворе c:
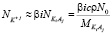 ,
,
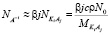 ,
,
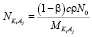 , (2)
, (2)
где, r – плотность раствора, N0 – постоянная Авогадро, 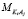 – молярная масса KiAj. Для чистой воды уравнение (1) выглядит следующим образом:
– молярная масса KiAj. Для чистой воды уравнение (1) выглядит следующим образом:
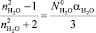 . (3)
. (3)
В разбавленном водном растворе можно принять следующее допущение:
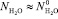
где, 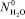 есть число свободных молекул воды в единице объема чистой, неразбавленной воды. Учитывая соотношения (2) и (3) в (1) получим:
есть число свободных молекул воды в единице объема чистой, неразбавленной воды. Учитывая соотношения (2) и (3) в (1) получим:
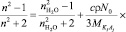
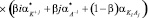 . (4)
. (4)
Принимая во внимание, что в разбавленных водных растворах вещество KiAj полностью диссоцирует на ионы b ≈ 1, уравнение (4) можно представить в следующем виде:
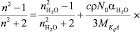
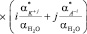 . (5)
. (5)
В первом приближении поляризуемость гидратированного иона можно взять пропорциональной кубу радиуса этого иона, а объем гидратированного иона можно представить как сумму объема негидратированного иона и объема гидратной оболочки:
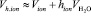 ,
,
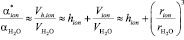 , (6)
, (6)
где, Vh.ion 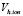 , Vion и
, Vion и 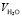 объемы гидратированного иона, негидратированного иона и молекулы воды, соответственно; hion число гидратации иона (катиона K+j или аниона A–i); rion и
объемы гидратированного иона, негидратированного иона и молекулы воды, соответственно; hion число гидратации иона (катиона K+j или аниона A–i); rion и 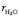 радиусы гидратированного иона данного типа и молекулы воды. Подставляя формулу (6) в (5) получим:
радиусы гидратированного иона данного типа и молекулы воды. Подставляя формулу (6) в (5) получим:
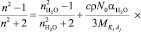
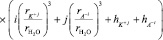 . (7)
. (7)
Воспользуясь уравнением (7) из графика зависимости отношения (n2 – 1)/(n2 + 2) от концентрации электролита c, по угловому коэффициенту графика tgj можно определить сумму чисел гидратации катиона K+j и аниона A–i в растворе при разных концентрациях KiAj:
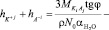
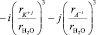 . (8)
. (8)
Результаты исследования и их обсуждения
Мы применяли эту модель для определения числа гидратации ионов в разбавленных водных растворах сульфата магния MgSO4 и солей калия KOH, KCl, KI, KIO3. Была измерена концентрационная зависимость показателя преломления разбавленных водных растворов сульфата магния на рефрактометре FR0429. Полученные данные в координатах (n2 – 1)/(n2 + 2) – c представлены на рис. 1. Как следует из рисунка до определенной концентрации сульфата магния (≈ 1,5 %) данная зависимость носит линейный характер, а выше этой концентрации наклон кривой уменьшается. Это можно объяснить тем, что при малых концентрациях сульфат магния полностью диссоцирует на ионы и эти ионы до концентрации ≈ 1,5 % не взаимодействуют между собой. Поэтому толщины гидратных оболочек и поляризуемости этих гидратированных ионов до указанной концентрации остаются постоянными и тем самым, как следует из формулы (7) в этой области угловой коэффициент tgj не будет зависеть от концентрации. При указанных концентрациях из-за сильной разбавленности раствора ростом плотности раствора можно пренебречь. При дальнейшем росте концентрации толщина гидратной оболочки 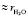 и соответственно, поляризуемости этих гидратированных ионов
и соответственно, поляризуемости этих гидратированных ионов 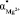 и
и 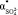 , а также плотность раствора r становятся зависимыми от с. Когда начинает проявляться взаимодействие ионов между собой, гидратные оболочки ионов начинают разрушаться, уменьшаются поляризуемости гидратированных ионов (
, а также плотность раствора r становятся зависимыми от с. Когда начинает проявляться взаимодействие ионов между собой, гидратные оболочки ионов начинают разрушаться, уменьшаются поляризуемости гидратированных ионов (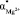 ,
, 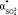 ), что проявляется в уменьшении углового коэффициента в вышеуказанной зависимости (рис. 1). По перегибу графика зависимости отношения (n2 – 1)/(n2 + 2) от концентрации электролита с можно определить пороговую концентрацию взаимодействия ионов между собой в данном растворе.
), что проявляется в уменьшении углового коэффициента в вышеуказанной зависимости (рис. 1). По перегибу графика зависимости отношения (n2 – 1)/(n2 + 2) от концентрации электролита с можно определить пороговую концентрацию взаимодействия ионов между собой в данном растворе.
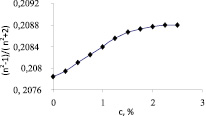
Рис. 1. Концентрационная зависимость отношения 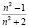 для водного раствора сульфата магния
для водного раствора сульфата магния
Подставляя взятых из литературы [1–3] значения параметров, (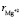 = 65 пм,
= 65 пм, 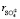 = 150 пм,
= 150 пм, 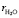 = 140 пм,
= 140 пм, 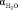 = 1,45×10–30м3, r ≈ 103кг/м3,
= 1,45×10–30м3, r ≈ 103кг/м3, 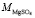 ≈ 0,12 кг/моль) входящих в формулу (8), по угловому коэффициенту графика представленного на рис. 1 мы определили сумму чисел гидратации ионов Mg2+ и
≈ 0,12 кг/моль) входящих в формулу (8), по угловому коэффициенту графика представленного на рис. 1 мы определили сумму чисел гидратации ионов Mg2+ и 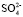 в водном растворе сульфата магния для следующих его концентраций:
в водном растворе сульфата магния для следующих его концентраций: 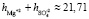 для концентраций c ≤ 1,5 %, tgj = 0,0559 и
для концентраций c ≤ 1,5 %, tgj = 0,0559 и 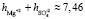 для концентраций 1,5 % < c < 2 %, tgj = 0,0224. Отметим, что концентрация c0 = 1,5 % является пороговой концентрацией взаимодействия ионов в водном растворе сульфата магния.
для концентраций 1,5 % < c < 2 %, tgj = 0,0224. Отметим, что концентрация c0 = 1,5 % является пороговой концентрацией взаимодействия ионов в водном растворе сульфата магния.
В книге Р. Робинсона и Р. Стокса [5] приведены значения чисел гидратации разных ионов определенных разными методами, где число гидратации для соли MgСl2 (что примерно равно числу гидратации иона Mg2+) по данным Барнартта [6] найдено равным 16–17. В работе [7] из концентрационных зависимостей коэффициентов диффузии молекул воды в растворах H2SO4 определено число гидратации иона 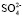 : 6. Сравнение значения суммы чисел гидратации ионов Mg2+и
: 6. Сравнение значения суммы чисел гидратации ионов Mg2+и 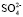 взятых из [6, 7] с полученными в нашей работе при концентрациях c < 1,5 %, tgj = 0,0559 показывает удовлетворительное согласие:
взятых из [6, 7] с полученными в нашей работе при концентрациях c < 1,5 %, tgj = 0,0559 показывает удовлетворительное согласие: 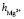 +
+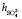 = = 16 + 6 =22.
= = 16 + 6 =22.
Показатели преломления разбавленных водных растворов солей калия KOH, KCl, Kİ и KİO3 были измерены рефрактометрическим методом в интервале концентраций 0 < c < 5 %. Если пренебречь концентрационной зависимостью поляризуемости и чисел гидратации ионов, что можно сделать при малых концентрациях растворимого вещества, то отношение (n2 – 1)/(n2 + 2) представляет из себя линейную функцию концентрации: (n2 – 1)/(n2 + 2) = A + Bc. Полученные из эксперимента значения параметров A и B для исследованных при температуре 25 °С, водных растворов (кроме водного раствора KOH) оказались следующими: для всех растворов A = 0,20422, , а значения В для KCl В ≈ 0,09, для Kİ В ≈ 0,055, а для KİO3 В ≈ 0,073. График зависимости отношения (n2 – 1)/(n2 + 2) от с для водного раствора KOH представлен на рис. 2. Видно что, для KOH линейность концентрационной зависимости (n2 – 1)/(n2 + 2) не выполняется. Для KOH пороговая концентрация взаимодействия ионов равна с0 = 3 %. На рис. 3 указан график зависимости суммы чисел гидратации иона калия и анионов OH-, Cl-, İ-и İO3 от суммы радиусов иона калия и соответствующих анионов построенного по табл. 1. Для проведения сравнений эти числа гидратации были определены при одинаковой молярной концентрации растворов (≈ 0,27 моль/л).
Таблица 1
Сумма чисел гидратации иона калия и анионов OH-, Cl-, İ- и İO3- при концентрации 0,27 моль/л и температуре 25 °С
|
Вещество |
r1 + r2, пм |
h1 + h2 |
|
KOH KCl KI KIO3 |
273 314 347 488 |
14,5 19,6, 21,01 [9] 26,1, 22,71 [9] 34,4 |
Через h1 обозначено число гидратации ионов калия, а через h2 – числа гидратации анионов OH-, Cl-, İ- и 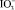 соответственно. Видно, что с ростом радиусов анионов сумма чисел гидратации ионов растет. Если число гидратации ионов калия во всех случаях принимать одинаково, то увеличение суммы можно объяснить ростом площади поверхности анионов с ростом их радиусов. Несмотря на одинаковость зарядов всех анионов в данном случае основную роль играет стерический фактор: с ростом радиусов анионов возникают новые позиции для размещения водных молекул на поверхности аниона и числа гидратации анионов растут по следующей последовательности: OH-, Cl-, İ- и İO3-. Значения чисел гидратации исследованных анионов, вычисленных по предложенному методу при принятии число гидратации иона калия равным 4 [5, 8], приведены на рис. 4 и в табл. 2. Тут же указаны числа гидратации этих ионов взятых из литературы [9] для проведения сравнения.
соответственно. Видно, что с ростом радиусов анионов сумма чисел гидратации ионов растет. Если число гидратации ионов калия во всех случаях принимать одинаково, то увеличение суммы можно объяснить ростом площади поверхности анионов с ростом их радиусов. Несмотря на одинаковость зарядов всех анионов в данном случае основную роль играет стерический фактор: с ростом радиусов анионов возникают новые позиции для размещения водных молекул на поверхности аниона и числа гидратации анионов растут по следующей последовательности: OH-, Cl-, İ- и İO3-. Значения чисел гидратации исследованных анионов, вычисленных по предложенному методу при принятии число гидратации иона калия равным 4 [5, 8], приведены на рис. 4 и в табл. 2. Тут же указаны числа гидратации этих ионов взятых из литературы [9] для проведения сравнения.
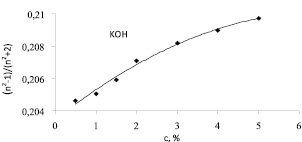
Рис. 2. Зависимость соотношения (n2 – 1)/(n2 + 2) от концентрации KOH в системе KOH + вода
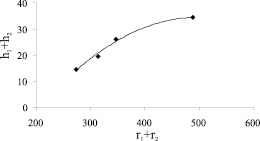
Рис. 3. Зависимость суммы чисел гидратации иона калия и анионов OH-, Cl-, İ- и İO3 от суммы радиусов иона калия и соответствующих анионов
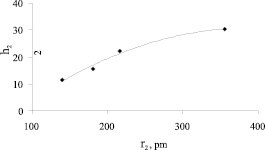
Рис. 4. Зависимость чисел гидратации анионов OH-, Cl-, İ- и İO3 от радиуса соответствующих анионов
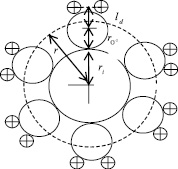
Рис. 5. Ион с гидратной оболочкой
Таблица 2
Числа гидратации анионов OH-, Cl-, İ- и İO3- при концентрации 0,27 моль/л и температуре 25 °С
|
Анион |
r2, pm |
h2 |
|
OH- Cl- İ- İO3- |
140 181 216 355 |
10,5 15,6 22,1 30,4 |
Наблюдается удовлетворительная корреляция между нашими и литературными данными. В работе [10] показано, что гидратация ионов, присутствующих в воде сильно влияют на валентные полосы комбинационного рассеяния воды и сила влияния анионов увеличивается в ряду: F– < 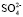 < Cl– < Br – < I– ≈
< Cl– < Br – < I– ≈ 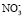 , что согласуется с результатами, полученными нашим методом.
, что согласуется с результатами, полученными нашим методом.
Числа гидратации каждого иона можно оценить предлагаемой нами, простой «ион-дипольной» моделью. В этой модели ион с гидратной оболочкой представляется в виде, как указано на рис. 5. В равновесном состоянии (месторасположение диполя на рисунке нарисовано пунктирной линией) потенциальная энергия данного диполя в поле иона и остальных диполей W = – pdE(r) уравновешивается с его кинетической энергией 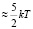 :
:
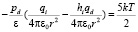 , (9)
, (9)
где, hi – число гидратации иона, 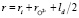 – расстояние между центрами иона и молекулой воды гидратной оболочки в равновесном положении, ri радиус рассматриваемого иона,
– расстояние между центрами иона и молекулой воды гидратной оболочки в равновесном положении, ri радиус рассматриваемого иона, 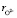 – радиус иона O2–, ld = pd/qd – длина диполя воды, pd – дипольный момент молекулы воды, qd = 2e – заряд диполя воды, qi заряд рассматриваемого иона, e – элементарный заряд, e0 – электрическая постоянная, e – диэлектрическая проницаемость раствора, k – постоянная Больцмана, T – абсолютная температура.
– радиус иона O2–, ld = pd/qd – длина диполя воды, pd – дипольный момент молекулы воды, qd = 2e – заряд диполя воды, qi заряд рассматриваемого иона, e – элементарный заряд, e0 – электрическая постоянная, e – диэлектрическая проницаемость раствора, k – постоянная Больцмана, T – абсолютная температура.
Из уравнения (9) можно определить число гидратации иона:
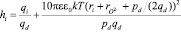 . (10)
. (10)
Расчет значения чисел гидратации ионов Mg2+ и 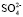 в водном растворе по формуле (10) (
в водном растворе по формуле (10) (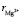 = 65 пм,
= 65 пм, 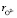 140 пм, pd = 6,13∙ ∙10–30 Кл∙м, e ≈ 81, Т ≈ 300 К) давал следующие значения:
140 пм, pd = 6,13∙ ∙10–30 Кл∙м, e ≈ 81, Т ≈ 300 К) давал следующие значения: 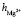 = 3,4,
= 3,4, 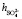 = 5,3,
= 5,3, 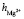 +
+ 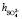 = 8,7. Последнее значение суммы чисел гидратации ионов Mg2+ и
= 8,7. Последнее значение суммы чисел гидратации ионов Mg2+ и 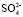 удовлетворительно согласуется со значением этой суммы определенном вышеуказанном рефрактометрическим методом при концентрациях 1,5 % < с < 2 %, tgj = 0,0224:
удовлетворительно согласуется со значением этой суммы определенном вышеуказанном рефрактометрическим методом при концентрациях 1,5 % < с < 2 %, tgj = 0,0224: 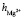 +
+ 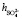 ≈7,46. Это означает что, уже при указанных концентрациях гидратные оболочки ионов становятся однослойными, как в «ион-диполной» модели. Вычисленные по формуле (10) значения чисел гидратации для ионов К+ и Na+ также хорошо согласуются со значениями чисел гидратации этих ионов определенными по скорости диффузии через мембрану Бринтцмигером [8]:
≈7,46. Это означает что, уже при указанных концентрациях гидратные оболочки ионов становятся однослойными, как в «ион-диполной» модели. Вычисленные по формуле (10) значения чисел гидратации для ионов К+ и Na+ также хорошо согласуются со значениями чисел гидратации этих ионов определенными по скорости диффузии через мембрану Бринтцмигером [8]: 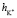 = 4,56,
= 4,56, 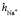 = 3,57.
= 3,57.
Библиографическая ссылка
Масимов Э.А., Аббасов Х.Ф. О РЕФРАКТОМЕТРИЧЕСКОМ ОПРЕДЕЛЕНИИ ЧИСЕЛ ГИДРАТАЦИИ ИОНОВ В РАЗБАВЛЕННЫХ ВОДНЫХ РАСТВОРАХ ЭЛЕКТРОЛИТОВ // Международный журнал прикладных и фундаментальных исследований. 2015. № 3-2. С. 181-185;URL: https://applied-research.ru/ru/article/view?id=6509 (дата обращения: 07.03.2026).

