Математическое моделирование процессов деформирования материалов (ковки, прокатки, резания и др.) с целью их усовершенствования сопровождается расчетом полей деформаций и напряжений в обрабатываемом изделии. Задача расчета деформирования однородных областей с помощью вариационного принципа скоростей и напряжений исследовалась В.Л. Колмогоровым и его учениками в работах [4, 5, 6]. В [1 ,2] построены варианты вариационного принципа для неизтормических процессов и для случая несимметричного тензора напряжений. В работе [3] приведен пример расчета напряженного состояния цилиндра с каналом.
Рассмотрим задачу о деформировании кусочно-неоднородной заготовки, занимающей объем V и состоящей из K подобластей 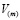 . Решение задачи проведем в лагранжевых переменных, так как рассматриваются большие деформации. В каждой подобласти введем локальную сопутствующую систему координат. Будем обозначать лагранжевы локальные переменные трехмерным вектором
. Решение задачи проведем в лагранжевых переменных, так как рассматриваются большие деформации. В каждой подобласти введем локальную сопутствующую систему координат. Будем обозначать лагранжевы локальные переменные трехмерным вектором 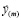 с компонентами
с компонентами 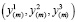 . Текущие координаты точек подобласти относительно неподвижной системы отсчета будем обозначать
. Текущие координаты точек подобласти относительно неподвижной системы отсчета будем обозначать 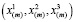 . Используем суммирование по умолчанию по повторяющимся индексам. Символ в скобках показывает номер подобласти. Суммирование по нему указывается явно. Поэтому номер подобласти располагаем где удобнее – вверху или внизу.
. Используем суммирование по умолчанию по повторяющимся индексам. Символ в скобках показывает номер подобласти. Суммирование по нему указывается явно. Поэтому номер подобласти располагаем где удобнее – вверху или внизу.
Будем считать, что материал подобластей однородный, изотропный, несжимаемый и выполняются гипотезы о подобии девиаторов напряжений и деформаций. Тогда свойства материала описываются функциями инвариантов:
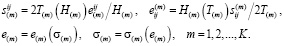 (1)
(1)
Здесь 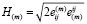 – интенсивность скоростей сдвига,
– интенсивность скоростей сдвига, 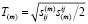 – интенсивность касательных напряжений,
– интенсивность касательных напряжений, 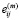 компоненты девиатора тензора скоростей деформации,
компоненты девиатора тензора скоростей деформации, 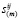 – компоненты девиатора тензора напряжений,
– компоненты девиатора тензора напряжений, 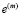 – первый инвариант тензора скоростей деформаций,
– первый инвариант тензора скоростей деформаций, 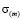 – первый инвариант тензора напряжений, m – номер подобласти.
– первый инвариант тензора напряжений, m – номер подобласти.
Предполагается, что поле скоростей 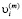 и поле напряжений
и поле напряжений 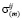 в пределах каждой подобласти непрерывны.
в пределах каждой подобласти непрерывны.
На внешней поверхности S области V заданы граничные условия:
на части поверхности 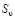 заданы скорости
заданы скорости 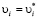 ;
;
на части поверхности Sf заданы внешние усилия 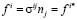 , где
, где 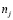 – компоненты вектора нормали к поверхности Sf ;
– компоненты вектора нормали к поверхности Sf ;
на части поверхности Ss задана сила трения 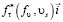 ,
, 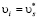 ,
, 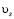 – скорость скольжения,
– скорость скольжения, 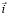 – единичный вектор в направлении скорости скольжения.
– единичный вектор в направлении скорости скольжения.
Звездочкой отмечены заданные функции.
Для поверхностей 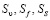 выполняются соотношения:
выполняются соотношения: 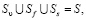 и
и 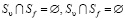 ,
, 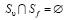 .
.
В случае неоднородной области на поверхностях контакта подобластей рассматриваются два варианта. Первый: прилипание – скорости непрерывны, для усилий выполняются условия равновесия. Пусть соприкасаются подобласти с номерами p и q. Тогда выполняются соотношения
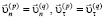 ,
,
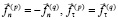 . (2)
. (2)
Здесь 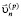 – компонента скорости по нормали к поверхности подобласти,
– компонента скорости по нормали к поверхности подобласти, 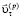 – касательная компонента скорости,
– касательная компонента скорости, 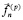 – компонента усилия на нормаль к поверхности подобласти,
– компонента усилия на нормаль к поверхности подобласти, 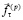 – компонента усилия, касательная к поверхности подобласти
– компонента усилия, касательная к поверхности подобласти 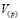 .
.
Второй – скольжение поверхностей. Поверхность скольжения подобластей 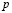 и
и 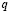 обозначим
обозначим 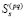 . В этом случае нормальные компоненты скоростей совпадают, так как тело сплошное, для нормальных компонент усилий выполняются условия равновесия:
. В этом случае нормальные компоненты скоростей совпадают, так как тело сплошное, для нормальных компонент усилий выполняются условия равновесия:
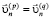 ,
, 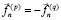 . (3)
. (3)
Разность касательных компонент скоростей равна скорости скольжения
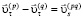 , (4)
, (4)
(номер в скобках совпадает с номером поверхности) разность касательных усилий определяется силой трения
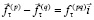 , (5)
, (5)
где 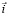 единичный вектор, направленный параллельно скорости скольжения
единичный вектор, направленный параллельно скорости скольжения 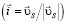 .
.
Для решения задачи используется вариационный принцип скоростей и напряжений [1, 2, 3]. Решение рассматриваемой краевой задачи может быть получено путем решения вариационного уравнения, записанного для произвольного фиксированного момента времени t, выражающего принцип виртуальных скоростей и напряжений. В случае неоднородной области имеет вид
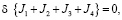 (6)
(6)
где
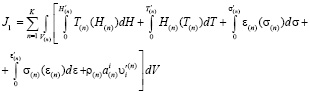
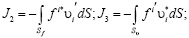
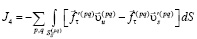 .
.
Суммирование в 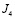 ведется по парам скользящих поверхностей p и q.
ведется по парам скользящих поверхностей p и q.
Приближенное решение в произвольный момент времени t по предложенному методу следует искать с помощью принципа (6) в виде линейной комбинации функций координат
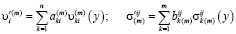 (7)
(7)
Здесь 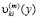 ,
, 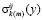 система линейно-независимых функций лагранжевых координат. Функции выбраны так, что
система линейно-независимых функций лагранжевых координат. Функции выбраны так, что 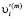 и
и 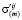 являются виртуальными. Коэффициенты
являются виртуальными. Коэффициенты 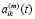 ,
, 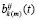 – варьируемые при фиксированном t функции времени; (в правой части (6) по повторяющимся индексам i, j суммирование не производится).
– варьируемые при фиксированном t функции времени; (в правой части (6) по повторяющимся индексам i, j суммирование не производится).
После подстановки (7) в (6) и варьирования, уравнение (6) превратится в систему обыкновенных дифференциальных уравнений относительно 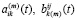 , которую дополняем условиями непрерывности скоростей и равновесия (2) или (3, 4) и условиями трения (5).
, которую дополняем условиями непрерывности скоростей и равновесия (2) или (3, 4) и условиями трения (5).
Рассмотрим классическую задачу обработки металлов давлением – ковку параллелепипеда плоскими штампами, которая рассматривалась неоднократно в аналогичной постановке [1–4]. Схема задачи показана на рис. 1. Показаны также глобальные оси координат и локальные оси для третьей области.
Для простоты будем считать, что заготовка состоит из прямоугольных слоев размера 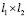 постоянной толщины
постоянной толщины 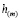 (
(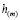 не зависит от y1, y2, но может меняться от слоя к слою). Предполагается, что в процессе обжатия все слои остаются прямоугольными, но могут деформироваться в усеченные пирамиды.
не зависит от y1, y2, но может меняться от слоя к слою). Предполагается, что в процессе обжатия все слои остаются прямоугольными, но могут деформироваться в усеченные пирамиды.
Пусть нижний штамп неподвижен, а верхний перемещается поступательно вниз со скоростью 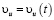 . Предполагается, что на контакте с инструментом превалирует зона скольжения Ss; зона прилипания SV, примыкающая к центру нижнего и верхнего оснований, практически отсутствует (
. Предполагается, что на контакте с инструментом превалирует зона скольжения Ss; зона прилипания SV, примыкающая к центру нижнего и верхнего оснований, практически отсутствует (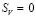 ). Предположим, что материал параллелепипеда обладает известными реономными свойствами, на контактной поверхности со штампами действует некоторый известный закон трения. Боковая поверхность параллелепипеда – это поверхность типа Sf, на которой
). Предположим, что материал параллелепипеда обладает известными реономными свойствами, на контактной поверхности со штампами действует некоторый известный закон трения. Боковая поверхность параллелепипеда – это поверхность типа Sf, на которой 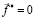 .
.
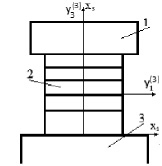
Рис. 1. Схема напряженно-деформированного состояния при осадке многослойного параллелепипеда: 1 – верхний штамп; 2 – заготовка; 3 – нижний штамп
Расчеты проводились для модели материала, для которой функции (1) имеют вид
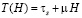 ,
, 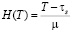 . (8)
. (8)
(бингамовский пластик).
Закон трения выбран по Зибелю [1,2]
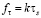 . (9)
. (9)
Очевидно, что закон трения (9) не зависит от скорости скольжения и не имеет обратной функции. В выражениях (8) и (9) 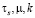 известные величины: предел текучести при чистом сдвиге, коэффициенты «вязкости» и трения соответственно.
известные величины: предел текучести при чистом сдвиге, коэффициенты «вязкости» и трения соответственно.
Будем предполагать, что физические координаты точек элемента имеют вид
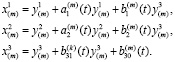 (10)
(10)
Такое представление перемещений позволит учесть возникающую в процессе деформации бочкообразность изделия. Вектор перемещений 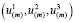 связан с вектором
связан с вектором 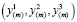 соотношениями
соотношениями
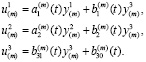
После подстановки (7, 8, 10) в (6) и варьирования получим систему относительно <<gorskiv69.wmf>> переменных. Часть переменных связаны и их можно исключить из системы, понизив порядок.
Считаем, что перемешивания материала между слоями заготовки нет, и поэтому уравнение неразрывности выполняется для каждого слоя. В лагранжевых переменных уравнение неразрывности примет вид
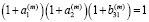 ,
,
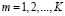 (11)
(11)
Предполагается, что слои деформируются без проскальзывания. Боковая внешняя поверхность заготовки непрерывная (без уступов). Следовательно, на боковой грани должны выполнятся соотношения
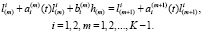
Отсюда получаем связь переменных 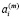 и
и 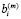
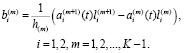 (12)
(12)
При деформировании заготовки слои не отделяются друг от друга. Поэтому должно выполняться равенство, связывающее переменные 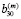 и
и 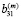
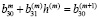 ,
, 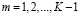 ,
,
и 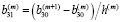 (13)
(13)
Используя соотношения (12, 13) исключим из системы уравнений переменные
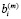 ,
, 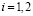 ,
, 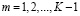 и
и 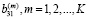 .
.
Чтобы исключить переменные 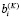 введем дополнительные переменные
введем дополнительные переменные 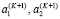 . Используя условие неразрывности (11) исключим из системы переменные
. Используя условие неразрывности (11) исключим из системы переменные 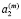 ,
, 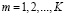 . Переменная
. Переменная 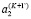 сохраняется. В итоге вектор переменных будет содержать следующие неизвестные функции
сохраняется. В итоге вектор переменных будет содержать следующие неизвестные функции
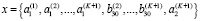 ,
,
всего 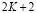 неизвестных. В итоге получим нелинейную систему обыкновенных дифференциальных уравнений, не разрешенную относительно старших производных, которую коротко можно записать в виде
неизвестных. В итоге получим нелинейную систему обыкновенных дифференциальных уравнений, не разрешенную относительно старших производных, которую коротко можно записать в виде
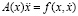
Здесь 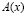 – матрица коэффициентов при вторых производных, блочная. Блоки трех-диагональные.
– матрица коэффициентов при вторых производных, блочная. Блоки трех-диагональные.
В случае однородной среды типа (8) можно ввести относительное время по формуле
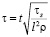 .
.
Очевидно, что при такой замене в модели будет только один существенный параметр – относительный коэффициент вязкости m. В случае неоднородной среды относительное время выберем из соотношения
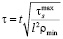 ,
,
где 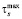 – максимальное значение
– максимальное значение 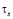 , а
, а 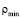 – минимальное значение
– минимальное значение 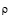 .
.
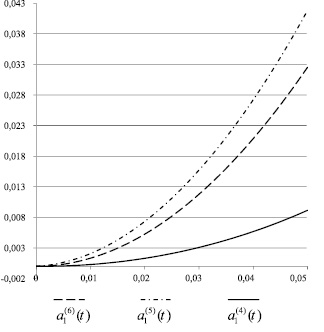
Рис. 2. Изменение параметров
Описанный алгоритм был опробован на модельном примере. Расчеты проводились при следующих начальных условиях:
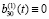 (нижнее основание неподвижно)
(нижнее основание неподвижно) 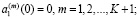
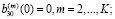
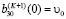 ,
,
где 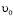 – заданная скорость бойка в момент касания.
– заданная скорость бойка в момент касания.
Относительные значения параметров
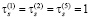 ,
, 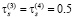 ,
,  .
.
Результаты решения представлены на рис. 2. Используется относительное время.
Такое соотношение параметров можно объяснить следующим образом: 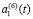 меняется меньше, чем
меняется меньше, чем 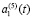 , так как влияет сила трения на поверхности контакта с инструментом; изменение
, так как влияет сила трения на поверхности контакта с инструментом; изменение 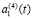 существенно меньше, так как сказываются силы инерции.
существенно меньше, так как сказываются силы инерции.
На рис. 3 тонкой линией показана исходная форма заготовки, жирной – форма после деформации. Пунктиром показано разделение заготовки на слои.
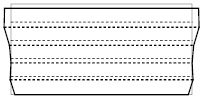
Рис 3. Изменение формы заготовки к моменту времени t=0,05 по сравнению с начальной формой
Рассмотренный вариант вариационного принципа скоростей и напряжений дает возможность учитывать неоднородность материала заготовки. Использованная форма представления перемещений позволяет учесть бочкообразность заготовки в процессе деформирования, что и продемонстрировано на примере расчета. Более точные расчеты могут быть выполнены с использованием более высокого порядка аппроксимации.
Библиографическая ссылка
Горшков А.В., Спевак Л.Ф. РЕШЕНИЕ ТРЕХМЕРНЫХ ЗАДАЧ ДЕФОРМИРОВАНИЯ НЕОДНОРОДНЫХ ОБЛАСТЕЙ МЕТОДОМ РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ, ОСНОВАННЫМ НА ВАРИАЦИОННОЙ ПОСТАНОВКЕ // Международный журнал прикладных и фундаментальных исследований. 2015. № 6-2. С. 218-223;URL: https://applied-research.ru/ru/article/view?id=6876 (дата обращения: 03.03.2026).

