Если неоднородная грунтовая среда в общем случае обладает свойством нелинейной ползучести, то зависимость между коэффициентом пористости и суммой главных напряжений в общем виде имеет вид
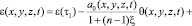
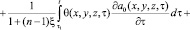
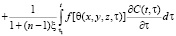 , (1)
, (1)
где
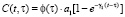 ; (2)
; (2)
ε(t), θ(t) – эти функции также изменяются по координатам x, y, z; f[θ(τ)] – функция, характеризующая нелинейную зависимость между коэффициентом пористости ε(t) и суммой главных напряжений θ(t) в скелете грунта; φ(τ) – функция старения; a1, γ1 – параметры ползучести; t1 – момент приложения внешней нагрузки; x – коэффициент бокового давления; а0 – коэффициент сжимаемости грунта, который в общем виде может зависеть от глубины исследуемой точки и времени; п – размерность рассматриваемой задачи; C(t, τ) – мера ползучести. Причем здесь функция f[θ(τ)] может изменяться в виде
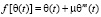 , (3)
, (3)
где μ – малый параметр.
Зависимость (1) при постоянных коэффициентах для одномерной задачи теории уплотнения однородных грунтов впервые была применена В.А. Флориным [6]. Он теорию упругоползучего тела Г.Н. Маслова-Н.Х. Арутюняна [1] смог применить к описанию процесса уплотнения глинистых грунтов, обладающих свойством ползучести. Экспериментальные исследования С.Р. Месчяна [4] доказали применимость этой теории к глинистым грунтам.
Функция старения φ(τ), в (2), обычно представляется в виде [1, 6].
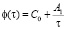 . (4)
. (4)
Здесь С0, А1 – опытные данные, τ – время приложения нагрузки.
Функции а0 и C(t, τ), характеризующие упруго-мгновенную деформацию и деформацию ползучести скелета грунта зависят от пространственных координат. Следовательно, выражение (1) можно представить так:
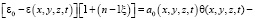
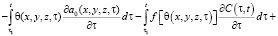
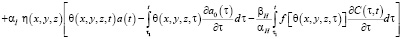 , (5)
, (5)
где
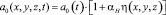 ; (6)
; (6)
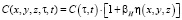 ; (7)
; (7)
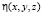 – функция пространственных координат, отражающая неоднородность грунта; αH и βH – параметры неоднородности, характеризующие упруго-мгновенную и ползучую деформации.
– функция пространственных координат, отражающая неоднородность грунта; αH и βH – параметры неоднородности, характеризующие упруго-мгновенную и ползучую деформации.
Выражение (5) при (6),(7) определяет изменение коэффициента пористости грунта в зависимости от суммы главных напряжений. Этим соотношением можно описать любое состояние скелета грунта. Если αH = 0, то имеем дело с нелинейной задачей однородного грунта. Когда 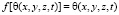 задача сводится к линейному состоянию грунта. Если αH = 0 и
задача сводится к линейному состоянию грунта. Если αH = 0 и 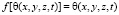 , то однородному состоянию грунта соответствует линейно-ползучее. Когда αH = 0, t = τ1 состояние грунта упругое.
, то однородному состоянию грунта соответствует линейно-ползучее. Когда αH = 0, t = τ1 состояние грунта упругое.
Процесс уплотнения трехфазной земляной среды без учета вязких свойств скелета и переменности коэффициента фильтрации согласно [6] описывается следующим образом
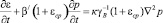 , (8)
, (8)
где – оператор Лапласа; εcp – средний коэффициент пористости; β/ и к – коэффициент объемного сжатия и фильтрации; γB – объемный вес воды; р – давление в поровой жидкости.
Учитывая соотношения (5) – (7) уравнение (8) приводим к следующему виду:
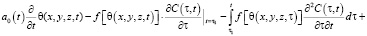
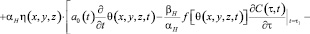
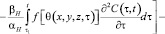
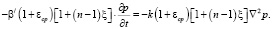 (9)
(9)
Если учесть соотношение [6], т.е.
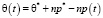 , (10)
, (10)
то уравнение (9) приводится к виду:
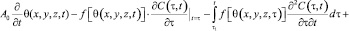
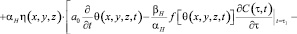
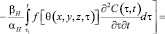
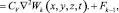 (11)
(11)
где θ* и p* – сумма главных напряжений и давление в поровой жидкости для стабилизированного состояния грунта;
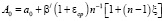 ;
;
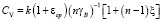 . (12)
. (12)
Дальнейшим функцию 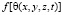 примем в виде полинома (3). Выражение (3) подставив в (11), затем решение полученного уравнения ищем в виде
примем в виде полинома (3). Выражение (3) подставив в (11), затем решение полученного уравнения ищем в виде
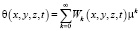 . (13)
. (13)
Тогда решение нелинейного интегро-дифференциального уравнения консолидации земляных масс (11) при (12) и (13) сводится к определению интегралов следующей системы линейных уравнений:
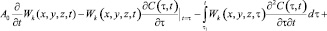
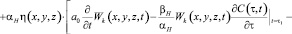
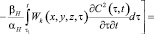
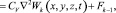 (14)
(14)
где
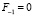 ;
; 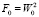 ;
;
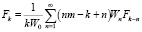 при m ≥ 1.
при m ≥ 1.
Таким образом, исследование нелинейной задачи механики уплотняемых неоднородных глинистых грунтов с учетом их ползучести при такой постановке сводится к решению линейных интегро-дифференциальных уравнений (14)
Следует заметить, что основное уравнение консолидации (11) получено в неявной форме по отношению к мере ползучести C(t, τ). В зависимости от C(t, τ) уравнения (14) естественно будет иметь различный вид. В данной работе в качестве этой функции примем следующее выражение:
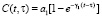 ,
,
тогда
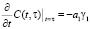 ;
;
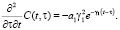
Подставив эти выражения в (14), получим реккурентную систему интегро-дифференциальных уравнений вида:
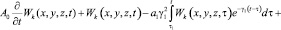
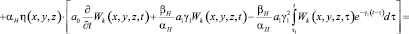
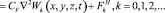 (15)
(15)
где
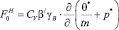 ;
; 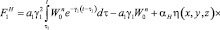
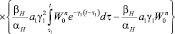 ;
;
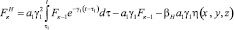
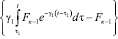 .
.
Итак, пусть требуется найти непрерывные функции Wk, удовлетворяющие в области 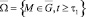 системе линейных дифференциальных уравнений (15) и краевым условиям общего вида
системе линейных дифференциальных уравнений (15) и краевым условиям общего вида
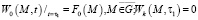 (16)
(16)
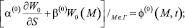
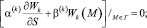 (17)
(17)
Здесь G – конечная область, ограниченная замкнутой кусочно-гладкой поверхностью Г ; S – внешняя нормаль к Г; 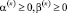 ;
; 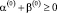 .
.
В целом данная задача относится к неоднородным краевым задачам теории консолидации упругоползучих грунтов с учетом их физической нелинейности. Решение этой задачи, безусловно, представляет большие трудности. Однако знание собственных значений 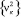 собственных функций
собственных функций 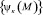 соответствующей однородной задачи позволяет решать и неоднородные задачи.
соответствующей однородной задачи позволяет решать и неоднородные задачи.
Решение уравнения (15) находим при помощи метода возмущений, успешно применяемого в теории упругости неоднородных тел [5]. Согласно этому методу введем некоторый малый параметр ρ т.е.
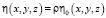 , (18)
, (18)
Здесь 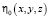 – некоторая непрерывная функция, отражающая неоднородность уплотняемого грунта.
– некоторая непрерывная функция, отражающая неоднородность уплотняемого грунта.
Решение уравнения (15) представим в виде:
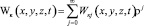 , (19)
, (19)
где 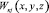 – некоторая непрерывная функция, подлежащая определению.
– некоторая непрерывная функция, подлежащая определению.
Для определения этой функции выражения (18) и (19) подставим в (15), затем приравнивая коэффициенты при ρ правой и левой части полученного равенства, находим следующую систему уравнений:
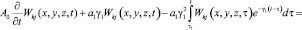
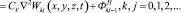 (20)
(20)
где
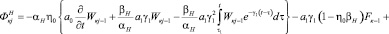
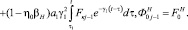
Решив систему линейных интегро-дифференциальных уравнений (20) при соответствующих начальных и граничных условиях находим неизвестные функции 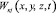 . Тогда согласно выражениям (13) и (19) сумма главных напряжений в скелете уплотняемого грунта представляется в виде:
. Тогда согласно выражениям (13) и (19) сумма главных напряжений в скелете уплотняемого грунта представляется в виде:
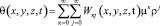 . (21)
. (21)
Распределение давлений в поровой жидкости 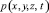 находится из выражения (10), т.е.
находится из выражения (10), т.е.
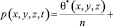
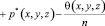 . (22)
. (22)
Здесь 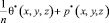 – давление в поровой жидкости, соответствующее начальному моменту времени.
– давление в поровой жидкости, соответствующее начальному моменту времени.
Осадку верхней поверхности уплотняемого массива находим из следующего выражения
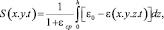 (23)
(23)
где 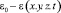 имеет вид (5).
имеет вид (5).
Таким образом, сумма главных напряжений в скелете грунта, давление в поровой жидкости и вертикальные перемещения верхней поверхности уплотняемого массива находятся соответственно из формул (21)-(23).
Ниже в качестве примера рассмотрим решение одномерной задачи консолидации неоднородных упругоползучих грунтов, где требуется определить напряжение в скелете грунта σ(z, t), давление в поровой жидкости р(z, t) и величину осадки S(t) уплотняемого массива неоднородного упругоползучего грунта конечной мощности. Расчетной схемой является слой грунта мощностью h в момент времени t = τ1, он подвержен действию распределенной нагрузки с интенсивностью q(z, t). Верхняя поверхность уплотняемого массива водопроницаема, а нижняя водонепроницаема.
Определение напряжений в скелете грунта σ(z, t) при n = 1 сводится к решению системы линейных интегро-дифференциальных уравнений, полученных из (18). Эти уравнения можно привести к дифференциальным уравнениям второго порядка. Для этого обе части (20) при n = 1 продифференцируем по времени, затем полученное выражение сложим с (20) предварительно умножив (20) на γ1. При этом получим:
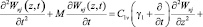
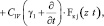 (24)
(24)
где
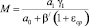 ;
;
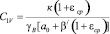 .
.
Уравнения (24) являются дифференциальными уравнениями второго порядка с постоянными коэффициентами M и C1V, которые зависят от свойств уплотняемого грунтового массива. Для решения их необходимо знать два начальных и граничных условий. Одно начальное условие имеет вид:
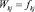 ,
, 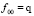 ,
, 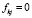 , (25)
, (25)
т.е. при t = τ1 вся нагрузка передается на жидкость. Второе начальное условие находится из (20) при t = τ1. Проделав это получим:
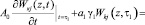
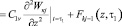 . (26)
. (26)
Граничными условиями рассматриваемой задачи будут:
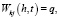
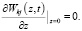 (27)
(27)
Решение (24), удовлетворяющее краевым условиям (25)-(27) получим в виде:
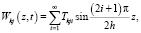 (28)
(28)
где
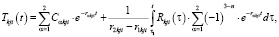
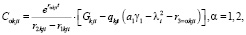
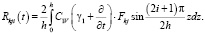
Здесь
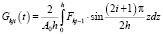 ;
; 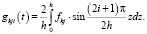
Величины r1kji, r2kji являются корнями уравнения:
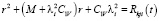 ,
,
где
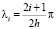 .
.
Выражение (28) подставив в (21) получим напряжение в скелете уплотняемого грунта, расчетная схема которого дана выше. Следовательно, расчетная формула для вычисления напряжений в скелете грунта имеет вид:
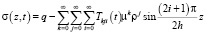 . (29)
. (29)
Расчетная формула (29) дает возможность учитывать влияния неоднородности среды и физической нелинейности ее формирования на напряженно-деформированное состояние уплотняемого массива. Причем численная реализация расчетной формулы (29) показала, что напряжение в скелете грунта в каждой точке уплотняемого слоя грунта, получается, по величине меньше на 10, 15 процентов, чем для однородного грунтового массива. Распределение порового давления и вертикальные перемещения точек верхней поверхности уплотняемого грунтового массива находятся из выражений (22),(23).
Следует заметить, что подобные задачи в другой постановке исследованы в [2–3].
Библиографическая ссылка
Юнусов А.А., Дасибеков А., Корганбаев Б.Н. РАСЧЕТ НЕЛИНЕЙНОЙ КОНСОЛИДАЦИИ ГРУНТОВЫХ ОСНОВАНИЙ // Международный журнал прикладных и фундаментальных исследований. 2015. № 10-1. С. 51-56;URL: https://applied-research.ru/ru/article/view?id=7381 (дата обращения: 05.01.2026).

