Предсказание субатомного состояния водорода весьма актуально для объяснения экспериментальных данных, полученных в области низкоэнергетических ядерных реакций [1–4]. Нам наиболее близок подход, развиваемый Ю.Л. Ратисом в работе [3], в которой показана возможность перехода начального состояния системы «электрон плюс протон» в относительно долгоживущий «нейтроний».
Покажем, что субатомные состояния атома водорода возможны, если справедлива формула де Бройля.
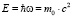 . (1)
. (1)
Смысл этой формулы заключается в том, что элементарная частица с массой покоя m0 представляет собой «сгусток» энергии, который должен двигаться по законам квантовой механики. В работе [5] показано, что использование выражения (1) для полной энергии частицы позволяет получить спектр квантования спина для квантовых частиц и их пространственную локализацию.
Субатомные состояния атома водорода возможны тогда, когда расстояния между протоном и электроном настолько малы, что перекрываются области их пространственной локализации, вызванные наличием собственной квантовой энергии движения.
Постановка задачи
Уравнение для отыскания энергии связи системы, состоящей из электрона (индекс 1) и протона (индекс 2) запишется в виде:
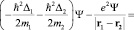
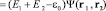 . (2)
. (2)
Здесь Е1 = m1c2, Е2 = m2c2 – собственные энергии электрона и протона, ε0 – энергия связи субатома. Система координат расположена в центре распределения вероятности системы из двух частиц. Если расстояния между электроном и протоном столь велики, что вклад областей их собственной локализации в энергию связи атома водорода исчезающее мал, то ε0 → 0:
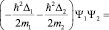
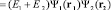 . (3)
. (3)
Далее решая это уравнение и считая Ψ1 и Ψ1 невозмущенными волновыми функциями задачи, можно вычислить в первом порядке теории возмущений вклад кулоновской энергии в энергию связи субатомного состояния.
Пойдем другим путем. В уравнении (2) попробуем «выключить» вклад движения протона в полную энергию системы и свести задачу к одноэлектронному виду. Учтем, что масса протона существенно превосходит массу электрона m2 >> m1 и комптоновская длина электрона r10 много больше комптоновской длины протона r20, r10 >> r20, где 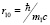 и
и 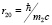 . Это неравенство позволяет поместить начало координат в центре локализации протона, поскольку собственная пространственная область локализации протона значительно меньше области собственной локализации электрона. Тогда из (2) имеем:
. Это неравенство позволяет поместить начало координат в центре локализации протона, поскольку собственная пространственная область локализации протона значительно меньше области собственной локализации электрона. Тогда из (2) имеем:
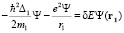 (4)
(4)
где δE = E1 – ε0. Внешне уравнение (4) напоминает задачу о традиционном атоме водорода, однако с одним принципиальным отличием dE > 0, поскольку энергия связи (здесь ε0 считается положительной) не может превосходить собственную энергию исходных частиц. Это приближение для двухчастичной квантовой системы в нашем случае несколько ущербно и главное не учитывает наличия спина у протона и не может предсказать орто- и парасостояний субатомного водорода. Поскольку δE > 0, то решение уравнения (4) не может дать обычного квантования энергии связи ε0. Однако можно оценить диапазон энергий, в котором находится ε0. Для решения уравнения (4) будем использовать подходы в задаче о «падающей» квантовой частице на силовой центр, описанной в [6].
Вычисление энергии связи для основного состояния
Для решения уравнения (4) используем сферическую систему координат и как обычно метод разделения переменных [6]. Представим Ψ(r, θ, φ) = R(r) Y(θ) Ф(φ), получим уравнения:
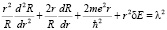 (5)
(5)
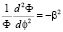 (6)
(6)
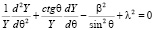 (7)
(7)
Сначала решаем уравнение (6). Его решение запишем в виде отличном от [6]:
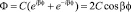 (8)
(8)
Здесь учитывается тот факт, что оба вращательных направления равновероятны, в результате имеем колебательные состояния по углу φ, а условие однозначности будет выполняться для составляющей плотности вероятности
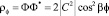 (9)
(9)
В результате имеем более общий ряд квантования: 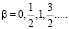 Далее примем
Далее примем 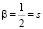 – это спин электрона фундаментальная величина, которая не должна изменяться во внешних полях, в том числе в поле протона.
– это спин электрона фундаментальная величина, которая не должна изменяться во внешних полях, в том числе в поле протона.
Найдем частное решение уравнения (7) для основного состояния в виде Y = sinθβ. Для констант разделения получим выражение λ2 = β(β + 1).
Для решения уравнения (5) введем безразмерную переменную 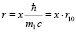
Получим:
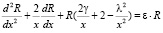 (10)
(10)
где 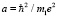 – боровский радиус атом водорода, a >> r10,
– боровский радиус атом водорода, a >> r10, 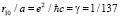 – постоянная тонкой структуры,
– постоянная тонкой структуры, 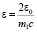 , λ2 = s(s + 1) 3/4.
, λ2 = s(s + 1) 3/4.
Решаем это уравнение методом возмущений, и учитываем, что кулоновская энергия взаимодействия мала по сравнению с собственной энергией электрона. Имеем для основного состояния электрона:
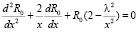 (11)
(11)
Проводя замену 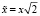 , и
, и 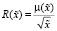 получаем уравнение Бесселя, которое при s = 1/2 имеет решение в виде функции Бесселя первого порядка
получаем уравнение Бесселя, которое при s = 1/2 имеет решение в виде функции Бесселя первого порядка
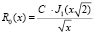 , (12)
, (12)
Это решение удовлетворяет граничным условиям. C – константа. R0(x) описывает неоднородную стоячую волну плотности вероятности. Можно видеть, что решение (12) отражает волновую природу движения квантовых частиц, заложенную в соотношении де Бройля (1).
Волновые решения обычно не нормируется. В связи с этим для интегральных вычислений необходимо использовать «обрезание» интегралов. Тогда в первом порядке теории возмущений имеем для энергии связи субатомного состояния:
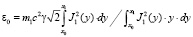 . (13)
. (13)
Плотность вероятности ρr = R20(x) имеет наибольший максимум в первой полуволне. Эту область и выберем как наиболее вероятную область локализации электрона. Тогда для верхнего предела J1(x1) = 0. Для нижнего предела в интегралах учтен тот факт, что в силу закона сохранения энергии собственная локализация электрона в начале координат запрещена. Решение уравнения (11) имеет смысл при выполнении соотношений:
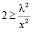 или
или 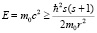 (14)
(14)
Полная энергия E является интегралом движения и есть сумма энергий радиального и вращательного движений. Тогда координата области от начала координат, в которой запрещено движение электрона, определяется как 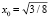 . Проводя численную оценку интегралов в (13), получаем ε0 ≈ 3,0∙103 эВ.
. Проводя численную оценку интегралов в (13), получаем ε0 ≈ 3,0∙103 эВ.
В обзорной работе [3] описаны результаты экспериментов по исследованию электрических взрывов фольг из особо чистых материалов в воде. В этой работе было обнаружено появление новых химических элементов и зарегистрировано «странное» излучение, которое не удалось идентифицировать (т.е., отнести к какому-либо из известных видов проникающей радиации). Напряжение на батарее конденсаторов, за счет разряда, который производились электрические взрывы, составляло ≈ 4,8 кВ. Электроны с такой энергией вполне могут стимулировать образование субатомного водорода в воде согласно оценкам по формуле (13). Заметим, что энергия связи субатомного состояния ε0 в 3 раза превышает верхний порог для энергии связи «нейтрония» [3], возможность образования которого предполагается в описанных выше экспериментах.
Развиваемый подход не может дать ответ на вопрос, как получит такое состояние водорода? Можно предположить, что электроны при столкновении с протонами должны иметь энергию вблизи ε0. В этом диапазоне энергий при образовании субатомов возможно возникновение тормозного излучения с максимально возможной энергией квантов до ~ ε0, Это излучение может проявляться в результате взаимного торможения при прохождении протона через электронное облако. Субатомный водород занимает значительно меньшую область локализации по сравнению с классическим атомом водорода и должен быть устойчив к внешним возмущениям, поскольку его электронная оболочка создана за счет собственной энергии движения электрона равной m1c2 = 5,6∙ 105 эВ. Время жизни такого субатома будет определяться внешней средой, поскольку существенно увеличена вероятность ядерных реакций.
Когда была закончена эта работа, стала доступна электронная версия статьи [7], в который автор проводит аналитический расчет системы «электрон + протон» со скачкообразным потенциалом, состоящем из кулоновской энергии и положительной модельной постоянной потенциальной энергии, Наличие постоянной составляющей энергии в принципе соответствует нашей задаче. Однако в нашем случае положительная энергия строго определена и равна собственной энергии электрона m1c2, кроме того учитываются спиновые состояния электрона.
Библиографическая ссылка
Неволин В.К. СУБАТОМЫ ВОДОРОДА // Международный журнал прикладных и фундаментальных исследований. 2015. № 10-5. С. 789-791;URL: https://applied-research.ru/ru/article/view?id=7627 (дата обращения: 11.02.2026).

