Абстрактная схема решения краевых задач применяется к исследованию существования обобщенных решений следующей краевой задачи:
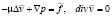в W, (1)
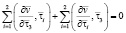на Г, (2)
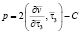на Г, (3)
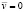на s. (4)
Здесь W – ограниченная область пространства R3, обладающая липшицевой границей, состоящей из конечного числа гладких поверхностей;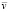 
– вектор смещений, p – гидростатическое давление, 
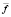– поле объемных сил; m – коэффициент Ламе; 
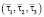– система координат.
Обозначим через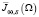 
линейную совокупность всех соленоидальных полей, обращающихся в ноль в окрестности гладкой части S границы 
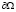. Замыкание в 
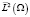этой совокупности обозначается через 
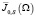, а замыкание в 
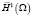через 
.
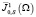Задача о нахождении обобщенных решений поставленной задачи сводится к решению задачи Коши для операторного уравнения
,
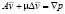где A – порождающий оператор гильбертовой пары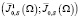 
.
Доказывается существование и единственность обобщенного решения задачи (1) – (4) о малых деформациях несжимаемой упругой среды под действием объемных сил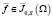 
, жестко закрепленной на части S границы 
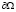и свободной от обобщенных напряжений на части Г. Доказывается, что при любом поле 
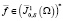существует слабое решение задачи.
Библиографическая ссылка
Веневитина С.С., Фурменко А.И., Уточкина Е.О. ИССЛЕДОВАНИЕ КРАЕВОЙ ЗАДАЧИ ТЕОРИИ МАЛЫХ ДЕФОРМАЦИЙ НЕСЖИМАЕМОЙ УПРУГОЙ СРЕДЫ // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 11-4. – С. 581-581;URL: https://applied-research.ru/ru/article/view?id=7795 (дата обращения: 23.11.2024).