Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Файлы

Сапронов И.В. 1 Зенина В.В. 1 Зюкин П.Н. 1

---

1 ФГБОУ ВО «Воронежский государственный лесотехнический университет им. Г.Ф. Морозова»

Статья в формате PDF

881 KB

Введем семейство банаховых пространств , :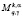

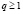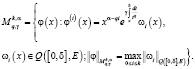
Рассматривается интегральное уравнение Вольтерра I рода вида

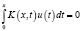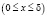, (1)

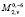в , где 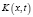– заданная функция со значениями в 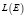, имеющая вид

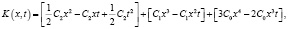(2)

где операторы 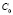, , 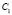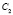являются ограниченными в .

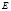Введем в рассмотрение операторный пучок

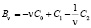. (3)

Теорема. Пусть выполнены следующие условия:

1) пучок (3) имеет характеристическое число ;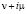

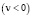2) характеристическому числу 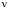соответствует собственный вектор 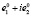и присоединенный вектор .

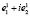Тогда для уравнения (1) существует решение вида

.

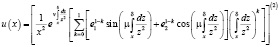Библиографическая ссылка