Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Файлы
• Литература

Спирина Н.М. 1 Сапронов И.В. 1 Зюкин П.Н. 1

---

1 ФГБОУ ВО «Воронежский государственный лесотехнический университет им. Г.Ф. Морозова»

Статья в формате PDF

830 KB

1. Гахов Ф.Д. Краевые задачи. – М.: Наука, 1977. – С.640.

Пусть область Dограничена кусочно-гладкой кривой Жорданаσ, лежащей в верхней полуплоскости y > 0 с концами в точках A(-a, 0), B(b, 0), a > 0, b > 0, и отрезком AB оси Ox.

Рассмотрим в области D вырождающееся эллиптическое уравнение

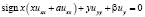. (1)

Задача. Пусть α, β – постоянные, такие что 0 < α < 1, 0 < β < 1, u(x, y) – дифференцируемая функция в области Dи дважды дифференцируемая в области 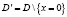, причём

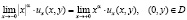.(2)

Также пусть u(x, y) удовлетворяет одному из следующих краевых условий

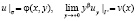(3)

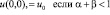, (4)

где v(x) – заданная непрерывная и ограниченная функция; u0 – заданная постоянная, .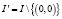

Теорема 1. Решение сформулированной выше краевой задачи единственно.

Теорема 2. Существует единственное решение сформулированной выше краевой задачи в треугольнике ABC и оно выражается явной формулой через заданные функции.

Библиографическая ссылка