Одной из актуальных задач является оценка качества лекарственных препаратов, выпускаемых разными фирмами. Спектрофотометрический метод успешно применяется для количественного определения содержания лекарственного препарата [1,3,7]. Однако в практике фармацевтического анализа чаще приходится иметь дело с препаратами сложного состава. Анализ таких лекарственных форм, которые содержат два и более компонента можно осуществить методами Уф-спектрофотометрии. Одним из таких способов является производная спектрофотометрия (ПСФМ), которая хорошо себя зарекомендовала при химических и биологических исследованиях [1,3].
Основным положительным эффектом «производных» спектров является увеличение разрешения перекрывающихся в исходных спектрах полос и снижение влияния фона [2,3]. Вторым преимуществом метода является резкое повышение контраста между полосами разной полуширины. Так маловыраженное поглощение при дифференцировании подавляется, а поглощение характерных полос даже слабой интенсивности усиливается [5]. Недостатком метода ПСФМ является ухудшение отношения сигнал : шум. Для уменьшения отношения сигнал : шум численное дифференцирование включает в себя многократное сглаживание исходных данных. На практике это означает вычисление производных высокого порядка, что приводит к большим трудозатратам и повышению вероятности ошибок в проводимых расчётах.
Материалы и методы исследования
Целью данной работы была разработка метода вычисления концентрации вещества в смеси, на основе производных спектров поглощения, с помощью компьютерной программы.
Предпосылкой для применения производной спектрофотометрии в количественном анализе является возможность описания полос поглощения определяемого вещества и примеси полиномами различных степеней. Если зависимость величины поглощения определяемого вещества от длины волны выразить уравнением многочлена (полинома):
Y = α0 +α1l + α2λ2 + …+ αnλn,
а поглощение примеси уравнением:
Y*= = b0 +b1l + b2λ2 + …+ bnλn,
то дифференцирование этих уравнений приводит к следующему. Если имеется фоновое поглощение постоянное по всему определяемому участку спектра, т.е. Y* = b0, то оно уничтожается при первом дифференцировании. Второе дифференцирование позволяет устранить влияние линейного фона. Влияние фона, описываемого полиномом “n” степени, можно устранить, если использовать производную “n+1” степени. Для нахождения значений производных спектра обычно используют уравнения многочлена вида:
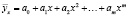 , (1)
, (1)
поскольку оно позволяет найти их с любой точностью. Необходимым условием наилучшего приближения будет минимизация суммы среднеквадратических отклонений
s = S(yi – y*(xi))2, (2)
где yi и y*(xi) – значения оптической плотности производной спектра поглощения и аппроксимирующего полинома.
Рекомендуется начинать с прямолинейного полинома 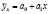 , а затем переходить к полиному 2-го порядка
, а затем переходить к полиному 2-го порядка 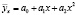 , а далее постепенно повышать порядок многочлена, до тех пор пока s не будет минимальной. Чебышев П.Л. разработал метод [4], значительно упрощающий весь процесс исчисления уравнения полиномов. Новый полином получался в виде суммы степеней, причём добавление новых слагаемых не изменяло вычисленных ранее коэффициентов.
, а далее постепенно повышать порядок многочлена, до тех пор пока s не будет минимальной. Чебышев П.Л. разработал метод [4], значительно упрощающий весь процесс исчисления уравнения полиномов. Новый полином получался в виде суммы степеней, причём добавление новых слагаемых не изменяло вычисленных ранее коэффициентов.
В этом случае уравнение производной спектра i-го порядка принимает вид (3), вместо (1):
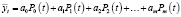 . (3)
. (3)
Формула для расчёта коэффициентов перед полиномами (4):
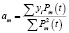 . (4)
. (4)
Числители параметров (4) определяются непосредственно. Знаменатели рассчитываются по следующей общей формуле (! – факториал, обозначающий последовательное умножение чисел натурального ряда, 3!= 1·2·3, 0!=1) (5):
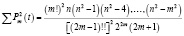 . (5)
. (5)
Выбор оптимального полинома осуществляют по наименьшему значению s (2).
Отсутствие программного обеспечения для вычислительных операций (1) – (5) не позволял широко использовать предложенный алгоритм расчёта. Нами была составлена компьютерная программа POLINOM.BAS для вычисления производных спектров высокого порядка на основе полиномов Чебышева. Программа составлена для персонального компьютера ПК, работающих в среде Microsoft Windows на программном языке Visual Basik. Алгоритм программы разработан в той же последовательности, которая изложена выше. Расчёт значений по формулам (1) – (5) в основном сводился к расчёту коэффициентов новой матрицы, которая являлась линейной комбинацией предыдущих. В целях упрощения работы с программой, она была составлена для расчёта коэффициентов полиномов Чебышева не превышающих восьмую степень. Ввод значений оптической плотности или коэффициентов поглощения через равные интервалы длин волн осуществляется с помощью клавиатуры вручную.
В нашей работе для спектрофотометрических измерений использовался спектрофотометр СФ-2000 – высокотехнологичный прибор, сочетающий в себе последние достижения в области оптики, электроники, точной механики и алгоритмизации вычислительных процессов. Прибор работает под управлением ЭВМ типа IBM PC, информация выводится на монитор в виде графиков спектров или в виде таблицы на печатающее устройство. Для определения концентрации веществ в смеси была приготовлена серия разведений модельной смеси папаверина гидрохлорида (ПГ) и дибазола (ДБ) с массовым соотношением 1:1, сняты спектры поглощения и рассчитаны производные 4, 6 и 8-ого порядков. Для построения градуировочных графиков были приготовлены растворы содержащие дибазол и папаверин гидрохлорид в разных концентрациях по 0,0002 %, по 0,0003 % и 0,0006 %. В качестве контрольного образца был использован чистый раствор папаверина гидрохлорида концентрацией 0,0005 %.
В качестве раствора сравнения и растворителя всех образцов применяли 0,0025 моль/л раствор кислоты хлороводородной. Собственных полос поглощения это вещество в диапазоне 190-400 нм не имеет. Спектры поглощения всех исследуемых растворов снимали с шагом 2 нм.
Для проверки применимости метода использовали таблетки «Папазол» трех производителей: Таблетки «Папазол» серии 71114 (годен до 12.2019), ОАО «Ирбитский химико-фармацевтический завод», г. Ирбит, Р №002068/01; Таблетки «Папазол» серии 003032014 (годен до 04.2019), ЗАО «МЕДИСОРБ», г. Пермь, Р №002815/01; Таблетки «Папазол» серии 40113 (до 02.2018), ОАО «УРАЛБИОФАРМ», г. Екатеринбург, Р №002246/01.
При предварительном изучении спектров поглощения растворов: папаверина гидрохлорида и дибазола, нами было выявлено, что дибазол имеет выраженный максимум при 238 нм (1,0822), а папаверина гидрохлорид – при 274 нм (0,189193) [6]. Однако спектр поглощения модельной смеси ПГ и ДБ показал, что полосы поглощения этих веществ накладываются друг на друга. Это делает невозможным непосредственное спектрофотометрическое определение ПГ и ДБ в смеси. Для идентификации веществ и дальнейшего их количественного определения в смесях необходимо разделить полосы поглощения, чтобы исключить влияние компонентов друг на друга, применяя производную спектрофотометрию. Такой анализ был проведён по каждому объекту исследования и по каждой производной. Ранее нами было установлено, что ПГ лучше определять по значению 4-ой производной при длине волны 276 нм, а ДБ – по значению 6-ой производной при длине волны 236 нм [6].
Результаты исследования и их обсуждение
Проведённое нами исследование в данной работе, зависимости величины шестой производной от концентрации дибазола в смеси, выявило линейную зависимость, что позволило получить калибровочный график (рис. 1). Зависимость значений 6-й производной от концентрации дибазола в модельной смеси представлена в табл. 1.
Таблица 1
Зависимость значений 6 производной от концентрации дибазола в смешанных растворах
|
Концентрация растворов с ДБ, % |
||||
|
0* |
0,0002 |
0,0003 |
0,0006 |
|
|
Значение производной 6-го порядка |
0* |
17604180 |
58366550 |
85077580 |
*Добавлена ещё одна точка с координатами (0,0). Ясно, что нулевой концентрации вещества будет соответствовать нулевое значение 4-й производной.
Этот график (рис. 1) можно использовать для определения концентрации дибазола в лекарственном препарате сложного состава по найденному значению шестой производной.
Построение калибровочного графика, нахождение уравнения линейной регрессии осуществляли с помощью компьютерной программы «Microsoft Office Excel 2007>Данные>Анализ данных>Регрессия».
Уравнение линейной регрессии
Y = – 495216 + 1,48 · 1011 · С,
где Y – значение шестой производной; С – концентрация смеси с дибазолом в %.
Коэффициент линейной корреляции в данном случае составил 0,998, что говорит об очень «сильной» линейной зависимости. Расчеты коэффициента корреляции осуществляли с помощью компьютерной программы «Microsoft Office Excel 2007> Данные >Анализ данных >Корреляция».
Используя полученной уравнение регрессии для дибазола, определяли концентрацию ДБ в растворах таблеток «Папазол» разных производителей по формуле:
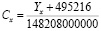 %,
%,
где Сх – концентрация ДБ в объекте исследования, Yх – значение производной 6-го порядка. Средняя абсолютная погрешность значения шестой производной составила 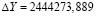 . Учитывая это, находим погрешность при определении концентрации дибазола по этой же формуле, составляет:
. Учитывая это, находим погрешность при определении концентрации дибазола по этой же формуле, составляет:
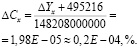
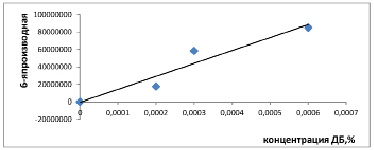
Рис. 1. График зависимости величины шестой производной от концентрации дибазола в смеси «Y = – 495216 + 1,48 × 1011 × С», где Y – значение шестой производной; С – концентрация модельной смеси с дибазолом в %. (Microsoft Office Excel 2007>Данные>Анализ данных>Регрессия)
Результаты проведённых расчётов представлены в табл. 2 «Концентрация ДБ и ПГ в таблетках «Папазол».
Для определения концентрации папаверина гидрохлорида в растворе модельной смеси, предварительно была доказана линейная зависимость значений производной четвёртого порядка от содержания папаверина в растворе. Проведя аналогичные расчёты, которые были осуществлены для ДБ, для ПГ была исследована зависимость 4-й производной от концентрации ПГ в модельной смеси. Был построен градуировочный график зависимости величины четвертой производной от концентрации папаверина гидрохлорида (рис. 2).
С помощью программы «Microsoft Office Excel 2007 > Данные > Анализ данных > Регрессия» получено уравнение регрессии Y = – 4878,43 + 1,09· 108· С. Используя найденное уравнение регрессии для папаверина, нашли концентрацию ПГ в растворах таблеток «Папазол» разных производителей:
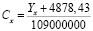 %,
%,
где Сх – концентрация ПГ в объекте исследования, Yх – значение производной 4 порядка. Средняя абсолютная погрешность значения четвёртой производной составила 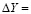 1624,05. Учитывая это, находили погрешность при определении концентрации папаверина по этой же формуле, т.е.
1624,05. Учитывая это, находили погрешность при определении концентрации папаверина по этой же формуле, т.е.
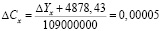 , %.
, %.
Результаты расчётов значений концентрации ПГ в таблетках «Папазол», предложенным методом, представлены в табл. 2.
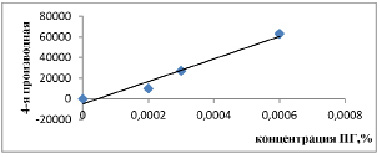
Рис. 2. График зависимости величины четвертой производной от концентрации папаверина гидрохлорида (Y = – 4878,43 + 1,09 ·108 · С), где Y – значение четвёртой производной; С – концентрация папаверина в сложном растворе в %. (Microsoft Office Excel 2007>Данные>Анализ данных>Регрессия)
Таблица 2
Концентрации ДБ и ПВ в таблетках «Папазол»
|
Объект исследования |
Концентрация ДБ % |
Концентрация ПГ % |
|
ОАО «Ирбитский химико-фармацевтический завод» |
(5,1±0,2)×10-4 |
(6,4±0,5)×10-4 |
|
Значение производной |
7,554878×107 |
57795,56 |
|
ЗАО «МЕДИСОРБ» |
(5,3±0,2)×10-4 |
(6,8±0,5)×10-4 |
|
Значение производной |
7,791056×107 |
60611,61 |
|
ОАО «УРАЛБИЛФАРМ» |
(5,4±0,2)×10-4 |
(6,98±0,5)×10-4 |
|
Значение производной |
8,011921×107 |
62287,73 |
|
Контрольный раствор * |
(5,2±0,5)×10-4 |
|
|
Значение производной |
51781,65 |
*В качестве контрольного раствора ПГ с концентрацией (0,0005 %) в растворе кислоты хлороводородной.
Результаты расчётов концентраций представленных в табл. 2, показывают, что концентрации дибазола в таблетках «Папазол», выпускаемые ЗАО «МЕДИСОРБ» и ОАО «УРАЛБИОФАРМ», укладываются в нормы допустимых отклонений от концентрации вещества, заявленной производителями (5,55×10-4 – 6,45×10-4 %). Рассчитанная нами концентрация дибазола в таблетках «Папазол» равная (5,1 ± 0,2 %), выпускаемых ОАО «Ирбитский химико-фармацевтический завод», оказалась чуть ниже нормы допустимых отклонений (6,0 ± 0,45 %).
Анализ табл. 2 показывает, что найденная нами концентрация папаверина гидрохлорида в таблетках «Папазол» разных фирм – производителей находится в соответствии с нормами допустимых отклонений от концентрации вещества, заявленной производителями (5,55×10-4–6,45×10-4 %).
Таким образом, анализ результатов использования метода производной УФ- спектрофотометрии для количественного определения веществ, входящих в состав препарата «Папазол», по разработанному нами алгоритму, позволяет определить их концентрацию с хорошей точностью. Использование компьютерных программ вычислительных операций снижает временные затраты на исследование и повышает точность производимого анализа.
Данная работа имеет и практическую значимость. Полученные нами результаты по анализу многокомпонентных смесей (МС) могут быть использованы в практической деятельности центров по контролю качества лекарственных средств, Бюро судебно-медицинской экспертизы, на кафедрах аналитической и фармацевтической химии высших учебных заведениях.
Библиографическая ссылка
Цокова Т.Н., Котлова Л.И., Осипова А.В. МЕТОД ПРОИЗВОДНОЙ УФ-СПЕКТРОФОТОМЕТРИИ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИИ ЛЕКАРСТВЕННОГО ПРЕПАРАТА В СМЕСЯХ // Международный журнал прикладных и фундаментальных исследований. 2015. № 11-5. С. 694-698;URL: https://applied-research.ru/ru/article/view?id=7865 (дата обращения: 24.02.2026).

