Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

Нами были проведены измерения продольной и холловской компонент тензора сопротивления (r_xx(B, T) и r_xy(B, T)) в перпендикулярных плоскости образца магнитных полях B = 0÷12,0 Тл и при температурах Т = (0,4÷80) К в наноструктурах n-InGaAs/GaAs с одиночными и двойными туннельно-связанными квантовыми ямами, так что различие между ними определялось только шириной барьера между ямами. Было проведено несколько серий измерений: эксперименты в интервале температур Т = (0,4÷80) К и магнитных полей B = 0÷12,0 Тл были проведены Центре низкотемпературной гальванометрии Института физики металлов УрО РАН на установке Oxford Instruments и при Т = (1,8÷80) К и B = 0÷9 Тл – на установке Quantum Design.

На рис. 1 представлены экспериментальные зависимости r_xx(B, T) и r_xy(B, T) для образца с одиночной квантовой ямой. В области слабых полей B < 0,8 Тл образец демонстрирует диэлектрическое поведение с температурой: r_xx(B, T) увеличивается при уменьшении T. При некотором значении магнитного поля Bc наблюдается температурно-независимая точка, положение которой смещается в меньшие поля с ростом температуры при T > 8 K. Видно, что эта точка находится в полях ВС = 0,83 Тл вблизи r_xx(B, T) = r_xy(B, T) (μВ = 1). В полях больших B_c уменьшается с уменьшением T. При В ≈ 0,9 Тл в образце начинаются осцилляции Шубникова-де Газа (с фактором заполнения v = 10 (см. вторую производную rxx(B, T) на рис. 1).

Итак, предметом нашего интереса является температурно-независимая точка B_c в области μВ = 1, которая в наших образцах «размывается» с ростом T, т.е. наблюдается B_c(T) (рис. 1). Такая температурная зависимость проводимости является необычной. Она наблюдалась и в более ранних работах [4], где авторами предпринимались попытки установить ее природу. Так, в работе [1 (Арапов, 2009)] было показано, что учет вкладов от слабой локализации и электрон-электронного взаимодействия в диффузионном 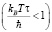и баллистическом 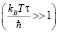(kB – постоянная Больцмана, τ – время свободного пробега, 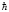– постоянная Планка) режимах проводимости в рамках теории [10 (и ссылки там)], учет влияния спиновых эффектов на электрон-электронное взаимодействие и учет осцилляций Шубникова-де-Гааза не приводит к появлению такой температурной зависимости проводимости. Для того, чтобы получить хорошее качественное совпадение расчетных зависимостей компонент тензора проводимости σxx(B, T) и σxy(B, T) с экспериментальными авторам [1 (Арапов, 2009)] пришлось прибегнуть к введению дополнительных линейных по T вкладов, как в диффузионном, так и в баллистическом режимах, причем решающую роль сыграл вклад в баллистическом режиме. В качестве механизмов проводимости, дающих появление такого линейного вклада, могут быть проводимость в параллельном канале (например, в барьерах) или проводимость, обусловленная температурно-зависимым экранированием [6], к которой обращались авторы работ [4] при объяснении полученных ими необычных зависимостей проводимости. Однако, полученные при этом параметры были далеки от теоретически предсказанных. Из неучтенных в [1, (Арапов, 2009)] механизмов температурной зависимости проводимости надо отметить поправку от электрон-электронного взаимодействия при рассеянии носителей на фриделевских осцилляциях электронной плотности вокруг примесей.

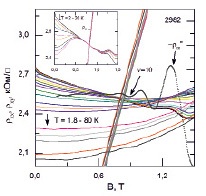
Рис. 1. Зависимости rxx(B, T) и rxy(B, T), при температурах T = 1,8–80 К для образца 2982 в слабых магнитных полях. На вставке: скорректированные зависимости r*xx(B, T) и rxy(B, T) (см. текст)

В [1 (Арапов, 2015)] было показано, что зависимость B_c(T) связана с температурной зависимостью подвижности m(T) носителей заряда. Если учесть эту температурную зависимость, и построить скорректированные компоненты тензора сопротивления r_*xx(B, T) и r_xy(B, T) (рис. 1), то видно, что в области μВ = 1 появилась ярко выраженная температурно-независимая точка, разделяющая две разные по проводящим свойствам фазы: «диэлектрическую» и «металлическую». Вблизи точки такого фазового перехода можно ожидать выполнения скейлинговских закономерностей [2] 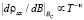где k – критический индекс. Мы извлекли критический индекс из наклона зависимостей 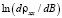от 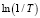, а затем экспериментальные значения r*xx были построены от скейлинговской переменной , как показано на рис. 2. Видно, что все кривые r*xx(B, T) разбиваются на две ветви и прекрасным образом ложатся одна на другую для всех температур T < 20 К. Начиная с T = 20 К эта закономерность нарушается (пунктирная кривая на рис. 2). Кроме того, следует обратить внимание на высокую симметричность относительно горизонтальной оси двух ветвей r*xx(B) на рис. 2. Все вышеперечисленное свидетельствует о том, что при B = Bc происходит фазовый переход изолятор – квантово-холловская жидкость с фактором заполнения n >2 (ν = n/nB, nB = eB/h – кратность вырождения уровня Ландау, e – заряд электрона, h – постоянная Планка). Таким же образом были определены значения k для всех образцов (таблица).

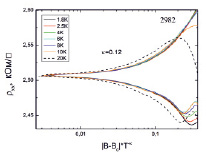
Рис. 2. Зависимости rxx от 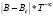при температурах T = 1,8–20 К для образца 2982

В рамках скейлинговских представлений, следующих из теории фазовых переходов и теории ренорм-группы, значение k определяется двумя факторами 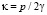, где p – показатель степени температурной зависимости длины фазовой когерентности 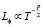, который зависит от механизма неупругого рассеяния, а g – критический индекс длины локализации x, которая определяет размер области, где электронные состояния локализованы. Гипотеза скейлинга [2] основана на предположении о степенной расходимости длины локализации ξ(E), когда энергия электронов E приближается к критической энергии фазового перехода E = Ec: 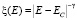или 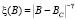. При реальных температурах размер области локализованных состояний задается длиной фазовой когерентности Lφ, когда x < L_φ – все состояния локализованы, в обратном случае – делокализованы.

Скейлинговские представления нашли прекрасное подтверждение при исследовании переходов между разными состояниями квантово-холловской жидкости, что соответствует переходам между плато квантового эффекта Холла [2]. Дискуссионным остается только вопрос об универсальности значений критических индексов k, p и g, которую предсказывает теория.

Теоретические представления о судьбе делокализованных состояний при уменьшении магнитного поля продолжают развиваться [8, 9]. В пионерских работах [9], основываясь на следующем из скейлинговой гипотезы предсказании [3], что в нулевом магнитном поле даже слабо разупорядоченная двумерная система невзаимодействующих электронов при нулевой температуре должна быть изолятором, было показано, что в слабых магнитных полях делокализованные состояния должны смещаться вверх по энергии («всплывать»), уходя на бесконечность по мере уменьшения B (гипотеза «всплывания»). В [8 (Huckestain, 2000)] утверждается, что переход изолятор – квантово-холловская жидкость из «диэлектрического» состояния в состояние с n > 2 в полном соответствии со стандартной скейлинговской теорией КЭХ определяет границы кроссовера между слабой локализацией (квантовые интерференционные эффекты в слабом магнитном поле) и сильной локализацией (КЭХ в квантующих магнитных полях). При этом, возможность наблюдения «всплывания» состояний существенно ограничена большой длиной локализации при экспоненциально малых температурах и экспоненциально малых размерах системы. Тем не менее, недавно в работе [8 (Mikhitaryan, 2010)] была предложена модель микроскопического описания этого перехода, согласно которой по разные стороны от него в пространстве разделяются области фазового действия магнитного поля, где оно влияет на интерференцию в процессе множественных актов рассеяния носителей заряда, и орбитального действия магнитного поля, где существенным становится изгиб траектории движения электрона и формирование циклотронной орбиты. В этой модели получен результат, подтверждающий сценарий «всплывания» и сделано количественное предсказание об удвоении критического индекса длины локализации g при «всплывании» делокализованных состояний.

Обсудим полученные нами количественные результаты для критического индекса k (таблица). Видно, что значения k уменьшаются с уменьшением ширины барьера в наших структурах. В литературе можно обнаружить значения k в интервале 0,15 до 0,82 [5, 7 (также см. ссылки там)]. В работе [5] показано, что k увеличивается от 0,3 до 0,8 с ростом концентрации электронов в структуре In0.52Al0.48As/In0.53Ga0.47As/In0.52Al0.48As при изменении напряжения на затворе, что объясняется усилением влияния дальнодействующего потенциала. Авторы [7 (Kim, 2004)] также показывают, что в квантовых ямах GaAs с самоорганизующимися квантовыми точками InAs, которые служат источником короткодействующего потенциала, отклонения значений k (причем как большую сторону k ≈ 0,47, так и в меньшую – k ≈ 0,15) от среднего значения k ≈ 0,33, полученного в широком интервале напряжений на затворе, наблюдаются только при самых больших концентрациях носителей, когда электроны эффективно экранируют рассеивающий потенциал, и он становится существенно дальнодействующим. Видно, что у нас никакой корреляции с изменением концентрации носителей нет. Корреляция полученных значений критических индексов k с изменением ширины барьера между ямами фактически означает связь с шириной самой квантовой ямы, поскольку в туннельно-прозрачных двойных квантовых ямах ширина ямы равна db + 2dw. Природа такого поведения пока не ясна: отклонение k к значениям больше универсального k = 0,42, полученного в пределе короткодействующего потенциала рассеяния [2], обычно связывают с влиянием крупномасштабного рассеивающего потенциала (см. примеры, описанные выше); отклонение k к значениям меньше универсального связано с уменьшением времени неупругого рассеяния электронов при увеличении степени беспорядка в системе.

Таким образом, нами проведены исследования квантового магнитотранспорта на серии структур с одиночной и двойными квантовыми ямами n-In_0.2Ga_0.8As/GaAs, отличающимися шириной барьера между ямами, в слабых магнитных полях в широком интервале температур Т = 0,4÷80 К. Показано, что существует критическое магнитное поле Bc, вблизи которого удалось провести масштабирование по температуре кривых r_xx(B,T), что соответствует наличию истинного фазового перехода изолятор – квантово-холловская жидкость. Обнаружено, что значение критического индекса, характеризующего этот переход, зависит от ширины барьера в структурах с двойными квантовыми ямами.

Работа выполнена в рамках государственного задания ФАНО России (тема «Спин», № 01201463330) при частичной поддержке программы фундаментальных исследований УрО РАН № 15-9-2-21.