Акустическая прозрачность цилиндрических трубопроводов различного назначения или отверстий в экранах определяется поперечными размерами отверстий и параметрами заполняющих их сред. Известно, что волны с длиной волны в среде более двойной ширины отверстия λ > 2d не могут проникнуть в область этого отверстия запредельная область длин волн).
Волновые процессы в трубопроводах имеют ту особенность, что движение сред, заполняющих трубопроводы, к изменению параметров направляемых волн, к невзаимности волноводных свойств структуры. Движения среды позволяет влиять на критические параметры структуры и позволяет управлять её прозрачностью.
Основные соотношения. Влияние движения среды рассмотрим для трубопровода прямоугольного поперечного сечения, сформированного жесткими границами, расположенными в плоскостях z = 0, z = d, y = 0, y = a (рис. 1. a, b). Волна распространяется вдоль оси 0x. Волновод заполнен изотропной средой, характеризуемой плотностью ρ и c – cкоростью распространения упругих волн в этой среде. Пусть среда движется со скоростью υ вдоль оси волновода 0x. Результирующая скорость волн в волноводе, определяется решением волнового уравнения для функции давления p(x,z) с учетом граничных условий при z = 0, z = d и различается для волн в прямом и в обратном направлениях, что может быть использовано для измерения скорости движения среды в волноведущих структурах [2, 3, 5].
В общем случае комплексная функция давления p(x,z) удовлетворяет уравнению Гельмгольца [4]:
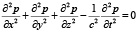 . (1)
. (1)
Граничные для компонент скорости смещения частиц условия на жестких поверхностях волновода имеют вид: vz(z = 0) = vz(z = d) = 0 [1]. Решение ищется в виде волны, распространяющейся вдоль оси волновода 0x и стоячей волны в поперечном направлении 0z. С учетом граничных условий имеем:
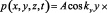
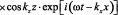 , (2)
, (2)
где 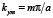 ,
, 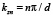 задаются граничными условиями, n, m = 0, 1, 2,… – номер моды. Подстановка этого решения в волновое уравнение дает известное дисперсионное соотношение:
задаются граничными условиями, n, m = 0, 1, 2,… – номер моды. Подстановка этого решения в волновое уравнение дает известное дисперсионное соотношение:
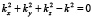 , (3)
, (3)
где 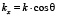 , θ – угол, под которым направлен волновой вектор, k зависит от направления распространения волны:
, θ – угол, под которым направлен волновой вектор, k зависит от направления распространения волны:
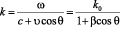 ,
,
где 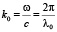 , λ0 – длина волны в свободном пространстве,
, λ0 – длина волны в свободном пространстве, 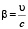 – относительная скорость среды. Дисперсионное уравнение (3) может быть представлено в виде уравнения для
– относительная скорость среды. Дисперсионное уравнение (3) может быть представлено в виде уравнения для 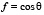 :
:
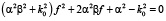 ,
,
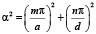 .
.
Распространение волн в волноводе с движущейся средой возможно при длине волны: λ ≤ λкр, где 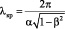 – критическая длина прямых и обратных волн с индексом m, зависящая от относительной скорости среды (рис. 2). Критические длины прямых и обратных волн совпадают.
– критическая длина прямых и обратных волн с индексом m, зависящая от относительной скорости среды (рис. 2). Критические длины прямых и обратных волн совпадают.
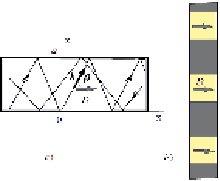
Рис. 1. Плоский волновод, заполненный подвижной средой
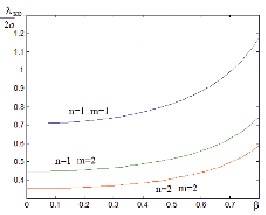
Рис. 2. Зависимость критических параметров от скорости среды
Основные результаты. Зависимость постоянной распространения прямых и обратных волн зависит от скорости движения среды:
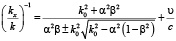 .
.
Для трех различных мод волн, распространяющихся в прямом и обратном направлениях, постоянные распространения как функции относительной скорости среды показаны на рис. 3. Из анализа следует, что движение среды в волноводе может приводить к увеличению числа распространяющихся мод. Моды, которые могут распространяться в волноводе с поперечным сечением axb определяются соотношением:
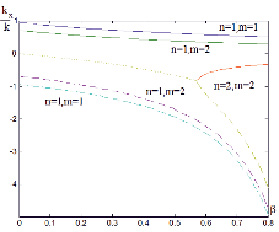
Рис. 3. Зависимость углов падения в прямом направлении для трех мод от скорости движения среды
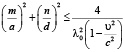 ,
,
где λ0 – длина волны в свободном пространстве. Различие параметров прямых и обратных волн растет с увеличением скорости движения среды в трубопроводе (рис. 3). С ростом скорости движения среды υ, заполнением волновода средой с малой скоростью распространения упругих волн c, увеличением размеров волновода a×d и частоты v увеличивается число мод m, n, для которых выполняется условие распространения.
При относительной скорости среды 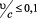 изменение скорости движения среды на 10 % приводит к изменению критического размера волновода на 1 %. Именение скорости движения среды с 0,6υ/c до 0,7υ/c приводит к изменению критического размера волновода на 12,5 %. С ростом скорости движения среды вдоль оси волновода критические длины прямых и обратных волн всех мод возрастают. Таким образом, непроницаемый в обычных условиях для акустических волн с длиной волны λ0 волновод или перфорированный экран (рис. 1) с поперечным размером a×a может стать проницаемым для нижшей моды, если среда его заполняющая приходит в движение со скоростью среды которая превосходит пороговое значение, которое можно найти из соотношения:
изменение скорости движения среды на 10 % приводит к изменению критического размера волновода на 1 %. Именение скорости движения среды с 0,6υ/c до 0,7υ/c приводит к изменению критического размера волновода на 12,5 %. С ростом скорости движения среды вдоль оси волновода критические длины прямых и обратных волн всех мод возрастают. Таким образом, непроницаемый в обычных условиях для акустических волн с длиной волны λ0 волновод или перфорированный экран (рис. 1) с поперечным размером a×a может стать проницаемым для нижшей моды, если среда его заполняющая приходит в движение со скоростью среды которая превосходит пороговое значение, которое можно найти из соотношения: 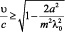 . Например, при a = λ0/4 (поперечные размеры волновода в два раза меньше критического значения, т.е. запредельное значение) в волноводе не распространяется в обычных условиях основная мода (m = 1, n = 1). Однако, если заполняющая волновод среда движется со скоростью
. Например, при a = λ0/4 (поперечные размеры волновода в два раза меньше критического значения, т.е. запредельное значение) в волноводе не распространяется в обычных условиях основная мода (m = 1, n = 1). Однако, если заполняющая волновод среда движется со скоростью 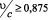 волновод вновь становится прозрачным для этой моды. Если же в волноводе в обычных условиях распространяется одна мода, то движение среды приводит дополнительно к возможности распространения высших мод.
волновод вновь становится прозрачным для этой моды. Если же в волноводе в обычных условиях распространяется одна мода, то движение среды приводит дополнительно к возможности распространения высших мод.
C увеличением скорости движения среды степень невзаимности структуры возрастает. В случае, когда скорость среды достигает скорости распространения волны в неподвижной среде (υ → c) структура приобретает свойство однонаправленности – одностороннее распространение волн (вентильный эффект). Скорость распространения волн в прямом направлении c + υ и равна 0 в обратном направлении.
Выводы
Установлено, что движение среды, заполняющей акустический волновод, приводит к невзаимности его параметров в прямом и обратном направлениях. Степень невзаимности пропорциональная скорости движения среды. Скорость движения среды также влияет на скорость распространения акустических волн и приводит к изменению критических частот или критических длин волн мод волновода. С ростом скорости движения среды увеличивается число мод, для которых выполняется условие распространения.
Библиографическая ссылка
Глущенко А.Г., Глущенко Е.П., Устинова Е.С. ВЛИЯНИЕ ДВИЖЕНИЯ СРЕД НА АКУСТИЧЕСКУЮ ПРОЗРАЧНОСТЬ ТРУБОПРОВОДОВ // Международный журнал прикладных и фундаментальных исследований. 2015. № 12-8. С. 1398-1401;URL: https://applied-research.ru/ru/article/view?id=8158 (дата обращения: 03.03.2026).

