Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Файлы

Спирина Н.М. 1 Сапронов И.В. 1 Веневитина С.С. 1

---

1 ФГБОУ ВО «Воронежский государственный лесотехнический университет им. Г.Ф. Морозова»

Статья в формате PDF

861 KB

Рассмотрим операторное уравнение второго рода с параметром λ

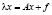. (1)

Здесь A оператор, действующий в банаховом пространстве E, полуупорядоченном конусом K; f – заданный элемент из пространства E.

Теорема 1. Пусть A – линейный положительный оператор и для некоторого элемента u0 > θ выполняется неравенство

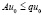, (2)

где 0 < q < λ, а элемент f ≥ θ удовлетворяет неравенству

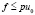. (3)

Пусть конус K нормальный. Тогда при всех f, удовлетворяющих неравенству (3), уравнение (1) имеет в K решение x*, к которому сходятся последовательные приближения

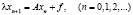(4)

при любом начальном приближении x0 ≥ θ, удовлетворяющем неравенству x0 ≤ au0 (a > 0). Кроме того, для решения x* уравнения (1) справедливы оценки

.

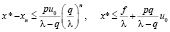Если в условиях теоремы 1 для некоторого элемента 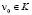выполняются неравенства 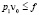, , 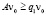где 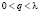, , 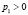то для решения x* уравнения (1) справедлива оценка

.

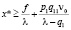Библиографическая ссылка