Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кульков В.Г. 1 Сыщиков А.А. 1

---

1 Филиал ФГБОУВО «Национальный исследовательский университет «МЭИ» в г. Волжском

На основе решения системы двух уравнений диффузии для границы и свободной поверхности пор находится величина избыточной по сравнению с равновесной концентрации зернограничных вакансий. Плотность источников вакансий в границе линейно связана со скоростью взаимного смещения смежных зерен вдоль общей границы. Модель описывает зависимость скорости такого смещения от величины механических напряжений, действующих в системе. Одним из важнейших параметров теории является взаимное соотношение диффузионных подвижностей вакансий на границах зерен и на свободной поверхности поры. Предложенный подход учитывает т.н. эффект подстройки напряжений. Давление распределяются на сегментах границ в соответствии с локальной величиной неравновесных вакансий. Рассматривается случай, когда контролирующим процессом является зернограничная диффузия по сравнению в поверхностной.

Статья в формате PDF

1407 KB

поры

зернограничная диффузия

пластическая деформация

концентрация вакансий

1. Глейтер Г., Чалмерс Б. Большеугловые границы зерен / Пер. с англ. – М.: Мир, 1975. – 375 с.

2. Кульков В.Г. Диффузионная модель внутреннего трения в нанокристаллическом материале // Журнал технической физики. – 2007. – Т. 77, № 3. – С. 43–48.

3. Кульков В.Г. Влияние динамического перераспределения примеси на зернограничное внутреннее трение в нанокристаллических материалах // Письма в Журнал технической физики. – 2005. – Т. 31, № 8. – С. 32–37.

4. Кульков В.Г. Межкристаллитное проскальзывание вдоль фасетированных границ зерен // Поверхность. Рентгеновские, синхротронные и нейтронные исследования. – 2005. – № 11. – С. 108–112.

5. Кульков В.Г., Жихарева М.Г. Проскальзывание по фасетированным границам зерен с учетом подстройки напряжения // Деформация и разрушение материалов. – 2005. – № 1. – С. 46–48.

6. Кульков В.Г. Взаимное движение зёрен вдоль границ с симметричными изломами // Конденсированные среды и межфазные границы. – 2001. – Т. 3, № 4. – С. 373–374.

7. Турков С.К., Шермергор Т.Д. Влияние подстройки напряжений на высокотемпературный фон внутреннего трения. – ФТТ. – 1965. – Т. 7, № 10. – С. 2952–2957.

Дифффузионные процессы на границах зерен в значительной степени определяют механизмы пластической деформации в поликристаллических металлических материалах. Структура этих границ в подавляющем большинстве не является совершенной, а содержит множество дефектов различной геометрической размерности. Современные технологии приготовления мелкозернистых материалов, такие, например, как консолидация порошков, равноканальное угловое прессование и др., неизбежно приводят к появлению остаточной пористости на границах зерен и в их тройных стыках. В настоящей работе рассматривается влияние зернограничных пор на скорость взаимного смещения смежных зерен при пластической деформации металлических образцов под действием приложенных к ним механических напряжений.

Рассмотрим фрагмент зеренной структуры, содержащий тройные стыки, представленный на рис. 1. В тройных стыках расположены цилиндрические поры, протяженные в нормальном к плоскости рисунка направлении оси z. Их сечения имеют вид окружностей. Границы считаем плоскими, вытянутыми в том же направлении и расположенными под взаимным углом π/2. Рассматриваемая зеренная структура носит название паркетной. Внешние напряжения приложены таким образом, что граница AB подвержена действию растягивающих напряжений σn, а граница A'B' – сжимающих напряжений – σn. На внутренней свободной поверхности поры напряжения отсутствуют. В установившемся режиме пластического движения верхней части образца по отношению к нижней между этими границами возникают диффузионные потоки вакансий, приводящие к перераспределению вещества. Аналогичные потоки имеются и в других тройных стыках. Пренебрегая диффузией в объем зерна, можно считать диффузионными зонами границу и сектор свободной поверхности поры AA'. Выпрямив диффузионный путь в ось x, сводим задачу к одномерной вдоль этой оси. Исходя из симметрии, достаточно рассмотреть участок OAC системы, который затем повторяется с чередованием знака источников. На рис. 2 представлен график зависимости плотности источника вакансий, соответствующий выбранному сегменту. Точки A и C имеют координаты a и a + b, где a и b – длины половины сечений границы и сектора поры.

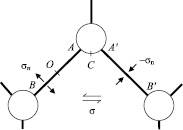
Рис. 1. Пора в тройном стыке

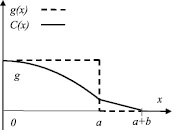
Рис. 2. Плотность источника и концентрация вакансий

Диффузионная задача для избыточной концентрации вакансий на границе и свободной поверхности поры в стационарном режиме имеет вид:

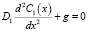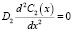, . (1)

,

,

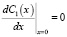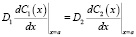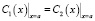. (2)

Здесь D1 и D2 – коэффициенты диффузии по границе зерен и по свободной поверхности, С1(х) и С2(х) – соответствующие концентрации неравновесных вакансий, g – плотность источника вакансий. Решением (1), (2) являются функции

,

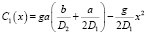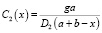. (3)

Связь избыточной С1(х) и равновесной C0 концентраций вакансий имеет вид [1, 2]:

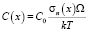, (4)

где Ω – объём вакансии, принятый равным атомному объему, k – константа Больцмана, T – температура.

Плотность источника вакансий можно найти, из следующих соображений [4]. За время Δt взаимное смещение зерен окажется равным υ?t (рис. 3). Объем материала, переходящего с границы A'B' на границу AB равен 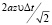, количество переместившихся вакансий. За то же время источник, работающий на этом сегменте границы с диффузионной толщиной δ создаст 2gδaz?t вакансий. Приравняв оба выражения, получим

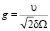. (5)

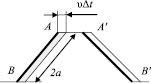
Рис. 3. Смещение границы за время Δt

Полная сила, приложенная к сегменту AB границы равна 2σnaz. Ее можно выразить через распределенное по сегменту границы нормальное напряжение σ(x).

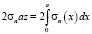. (6)

Выражение (6) учитывает так называемый эффект подстройки напряжений [5, 7]. Выразив из (4) σn(x) и подставив его в (6) с учетом (3) и (5), получим

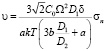. (7)

Если рассматривать фасетированную границу зерен с плоскими фасетками, наклоненными к средней плоскости ее залегания под углами ± π/2, с порами в местах сопряжения фасеток, то ситуация аналогична рассмотренной. Выражение (7) можно переписать в этом случае в виде

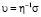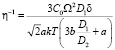, . (8)

Здесь учтено, что нормальное напряжение σn на фасетках связано со сдвиговым напряжением σ, действующим вдоль направления, проходящего через центры пор (рис. 1) как σ = 2σn. Коэффициент η–1 представляет собой обратную сдвиговую вязкость. В большинстве случаев коэффициент поверхностной диффузии значительно превышает коэффициент зернограничной диффузии. Используя соотношение 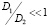, для обратной сдвиговой вязкости из (8) получим выражение

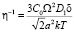. (9)

Выражения типа (9) обычно описывают проскальзывание по межзеренной границе в случае, когда определяющим механизмом является наличие диффузионных граничных потоков вакансий [1, 6]. Описанная модель применима в случае, когда не нарушается целостность поры. Это условие выполняется при достаточно высоких температурах, когда диффузия вдоль поверхности поры настолько велика, что ее форма не изменяется при взаимном пластическом смещении зерен.

Библиографическая ссылка