Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Водахова В.А. 1 Тлупова Р.Г. 1 Эржибова Ф.А. 1 Болова Д.А. 1

---

1 Кабардино – Балкарский государственный университет им. Х.М. Бербекова

Нагруженные уравнения в частных производных гиперболического, параболического, эллиптического и смешанного типов находят большое применение как метод математического моделирования нелокальных, в том числе фрактальных, процессов и явлений, и метод эффективного поиска приближенных решений дифференциальных уравнений. Математической основой физики фракталов, в особенности дробной динамики, стали нагруженные дифференциальные уравнения, демонстрирующие роль этих уравнений в различных отраслях современной науки, в частности, в математической биологии, физики, химии, инженерной технологии. Настоящая статья посвящена постановке и исследованию однозначной разрешимости одной нелокальной краевой задачи для смешанного нагруженного параболо – гиперболического уравнения третьего порядка. При доказательстве единственности решения поставленной задачи в работе рассматривается три случая: когда дискриминант характеристического уравнения S = 0, S > 0 и S < 0. В случае S = 0 приводится доказательство единственности решения поставленной задачи, а в случаях S > 0 и S < 0 доказательство проводится аналогично. Вопрос существования решения поставленной задачи редуцирован к вопросу разрешимости системы интегральных уравнений Вольтерра второго рода относительно следа искомого решения, которая однозначно разрешима.

Статья в формате PDF

1438 KB

краевая задача

система интегральных уравнений Вольтерра второго рода, смешанное нагруженное уравнение

уравнение гиперболо – параболического типа

преобразование Лапласа

1. Водахова В.А. Нелокальная краевая задача для нагруженного уравнения третьего порядка с кратными характеристиками. В сборнике: Математическое моделирование и краевые задачи. Труды четвертой Всероссийской научной конференции с международным участием. – 2007. – С. 57–60.

2. Водахова В.А. Об одной краевой задаче для уравнения третьего порядка с нелокальным условием А.М. Нахушева. // Дифференциальные уравнения, 1983. – Т. 19. № 1. – С. 163–166.

3. Водахова В.А., Гучаева З.Х. Задача Дирихле для смешанного параболо – гиперболического уравнения с разрывными коэффициентами. Успехи современного естествознания. – 2013. – № 11. – С. 136–140.

4. Водахова В.А., Гучаева З.Х. Нелокальная задача для нагруженного уравнения третьего порядка с кратными характеристиками. Успехи современного естествознания. – 2014. – № 7. – С. 90–92.

5. Водахова В.А., Тлупова Р.Г., Шерметова М.Х. Внутреннекраевая задача для нагруженного уравнения третьего порядка с кратными характеристиками. Успехи современного естествознания. – 2015. – № 1-1. – С. 71–75.

6. Езаова А.Г., Думаева Л.В. Об одной внутренне – краевой задаче для уравнения третьего порядка с группой младших членов. Фундаментальные исследования. – 2015. – № 2-27. – С. 6032–6036.

7. Нахушев А.М. Нагруженные уравнения и их приложения. / Научн. – исслед. инс – т прикладной математики и автоматизации КБНЦ РАН. – М.: Наука, 2012. – 232 с.

8. Нахушев А.М., Краевые задачи для нагруженных интегро- дифференциальных уравнений гиперболического типа и некоторые их приложения к прогнозу почвенной влаги // Дифференциальные уравнения, 1979. – Т. 15. № 1. – С. 96–105.

9. Репин О.А., Кумыкова С.К. О задаче с обобщенными операторами дробного дифференцирования для уравнения смешанного типа с двумя линиями вырождения // Вестник Самарского государственного технического университета. Серия «Физико – математические науки». – 2013. – № 1(30). – С. 150–158.

10. Репин О.А., Кумыкова С.К. Об одной нелокальной задаче для уравнения смешанного типа третьего порядка с кратными характеристиками // Дифференциальные уравнения. – 2015. – Т. 51. № 6. – С. 755–763.

Нагруженным уравнением в частных производных второго порядка посвящены работы [1-10]. Общее определение этого широкого класса уравнений в частных производных было впервые дано А.М. Нахушевым в работах [7-8].

Многими авторами исследовались нелокальные краевые задачи для смешанных эллиптико – гиперболических и гиперболо – параболических уравнений второго порядка. Нелокальные краевые задачи для смешанного и смешанного нагруженного гиперболо – параболического типов уравнений более высокого порядка, то они остаются мало исследованными.

Цель работы состоит в постановке и исследовании однозначной разрешимости одной нелокальной краевой задачи для смешанного нагруженного уравнения третьего порядка.

Постановка задачи. Пусть Ω – конечная односвязная область, ограниченная отрезками AA0, А0B0, BB0 прямых x = 0, y = h, x = l соответственно, расположенных в полуплоскости y > 0, и характеристиками

AC:x + y = 0, BC:x – y = l

уравнения

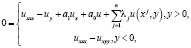(1)

Ω1 – параболическая, а Ω2 – гиперболическая части области Ω.

Предполагается, что 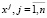– фиксированные точки из интервала (0, l), причем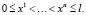

Задача. Найти функцию u(x, y) со следующими свойствами:

1) ;

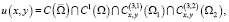
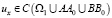2) u(x, y) – регулярное решение уравнения (1) при y ≠ 0;

3) u(x, y) – удовлетворяет краевым условиям

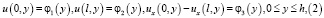
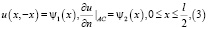
где

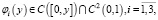
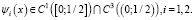
Переходя к пределу в уравнении (1) при y → + 0, получим функциональное соотношение между u(x, 0) = τ(x) и uy (x, 0) = v(x), принесенное из параболической части Ω1 на линию y = 0, в виде

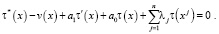(4)

Общее решение уравнения (1) при y < 0 задается формулой

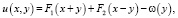(5)

где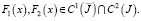

Удовлетворяя (5) краевым условиям (3), получим систему уравнений

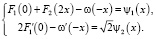
Определим из второго уравнения системы ω(– x):

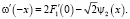
Интегрируя, получим

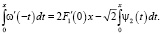
Отсюда, что то же самое

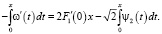
и, окончательно,

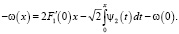
Подставляя ω(– x) в первое уравнение системы, найдем

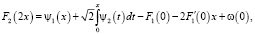
или

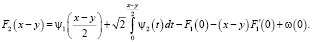
Из (5) будем иметь

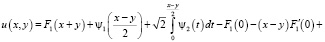
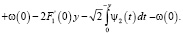
В результате несложных преобразований последнее принимает вид

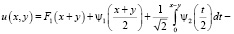
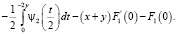(6)

Дифференцируя (6) по x, а затем по y, и вычитая из первого соотношения второе и переходя к пределу при y → – 0, получим функциональное соотношение между τ(x) и v(x), принесенное из гиперболической части Ω2 на линию y = 0 в виде

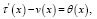(7)

где

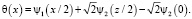
Исключая v(x) из (4) и (7), с учетом граничных условий (2), получим для определения τ(x) следующую задачу:

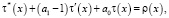(8)

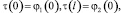
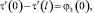(9)

где .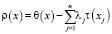

Характеристическое уравнение, соответствующее однородному уравнению

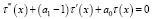(8')

имеет вид

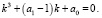(10)

Введем обозначение 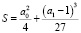. Известно [2], что уравнение (10) имеет один действительный и два комплексно-сопряженных корня, если S > 0. Оно имеет три различных действительных корня, если S < 0. При S = 0 все три корня уравнения (10) действительны, причем два из них равны.

Пусть S = 0, т.е. 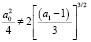. В этом случае имеем, что

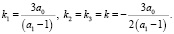
Так как общее решение уравнения (8') в этом случае имеет вид

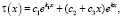
методом вариации постоянных, находим общее решение уравнения (8) в виде

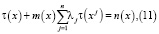
где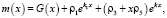

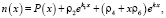
причем, G(x), P(x),ρi – известные функции.

Полагая в равенстве (11) поочередно x = x1, x = x2,…, x = xn, получаем следующую систему алгебраических уравнений относительно τ(x),

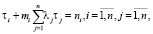(12)

где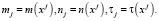

При выполнении условия

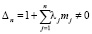(13)

система (12) имеет единственное решение

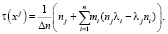(14)

Таким образом, подставляя (14) в (11), находим единственное решение задачи (8), (9). Легко заметить, что τ(0) ≡ 0, если .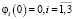

После определения функции τ(x) мы приходим к задаче (2), u(x, 0) = τ(x) в области Ω1. Допустим, что однородная задача имеет нетривиальное решение v(x, y). Положим

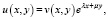(15)

где λ, μ – некоторые постоянные. Для функции v(x, y) получим уравнение

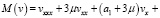
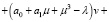
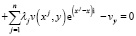
и краевые условия

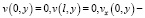
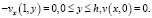(16)

По предположению, в силу (15), эта задача имеет нетривиальное решение v(x, y).

Рассмотрим тождество

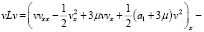
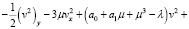
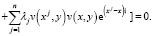
Интегрируя это тождество по области Ω1 и учитывая однородные граничные условия (16) получим

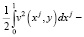
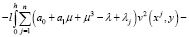
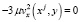(17)

Выберем λ и μ так, чтобы 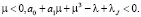При таком выборе λ и μ левая часть равенства (17) становится строго положительной, что невозможно, если v(x, y) ≠ 0. Отсюда следует, что v(xj, y) = 0. Отсюда будем иметь, что v(xj, y) ≡ 0 для всех 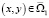, и, согласно (15), u(x, y) ≡ 0 для всех 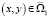. В области Ω2 однородная задача v(x, 0) = 0, 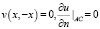для уравнения (1) при y < 0 имеет только тривиальное решение u(x, y) ≡ 0 для всех 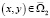. Следовательно, u(x, y) = 0 в Ω2.

Для доказательства существования решения поставленной задачи рассмотрено уравнение

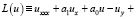
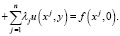(18)

Доказано, что при

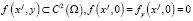
краевая задача

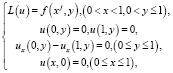(19)

имеет решение.

Существование решения задачи (18), (19) устанавливается с помощью преобразования Лапласа и сведением задачи к системе интегральных уравнений Вольтерра второго рода, относительно следа искомого решения, которая однозначно разрешима.

Библиографическая ссылка